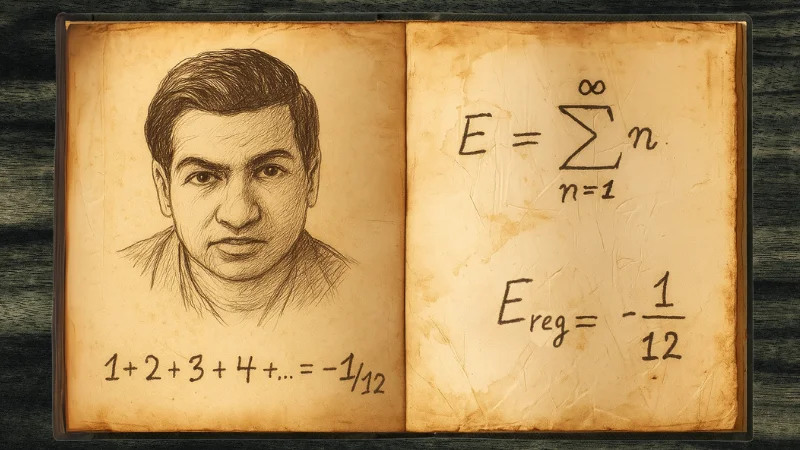A simple vista, sumar todos los números naturales (1 + 2 + 3 + 4 + 5 + …) parece conducir a un resultado obvio: el infinito. ¿Cómo podría ser de otra forma? Cada número suma más que el anterior, y no hay final. Sin embargo, en algunos contextos matemáticos y físicos aparece una afirmación tan desconcertante como fascinante:

¿Una paradoja? ¿Un error? ¿O una muestra de que las matemáticas pueden ir más allá de la intuición?
Sumas divergentes y función zeta
En matemáticas clásicas, esta serie es claramente divergente. Es decir, su suma crece sin límite:
![]()
Pero hay un contexto en el que esta suma puede adquirir un valor finito de forma formal y coherente. La clave está en una herramienta poderosa: la función zeta de Riemann.
Para s>1, la función zeta se define como:

Y cuando se extiende mediante continuación analítica, se puede evaluar para otros valores de s. Por ejemplo:

⚠️ Importante: esto no significa que la suma 1 + 2 + 3 + 4 +… sea literalmente –1/12 en el sentido habitual. Es una asignación formal dentro de un marco extendido de análisis complejo, útil en contextos específicos de la física teórica.
Ramanujan y las series imposibles
El matemático indio Srinivasa Ramanujan escribió este resultado en sus cuadernos a principios del siglo XX. En una carta a Hardy decía que:

Hardy, inicialmente escéptico, acabaría demostrando que, bajo ciertos métodos de regularización de series divergentes, ese valor era matemáticamente consistente. El resultado fue polémico durante décadas, hasta que la física vino a rehabilitarlo.
¿Y por qué aparece en física?
En teoría de cuerdas bosónica, los modos vibratorios de una cuerda se modelan como una suma infinita de energías:

Este valor es, de nuevo, infinito. Pero al regularizar esta suma mediante métodos como la zeta de Riemann, se obtiene:

Este valor, sorprendentemente, no solo no rompe la física, sino que la hace funcionar. De hecho, es clave para que las ecuaciones de la teoría de cuerdas sean consistentes con la relatividad. Gracias a este término, se fija que el número mínimo de dimensiones necesarias para que funcione la teoría es 26.
¿Es esto magia matemática?
No. Es rigor llevado más allá de la intuición habitual. Para entenderlo mejor, piensa en una analogía:
En óptica, un espejo cóncavo puede hacer converger rayos que originalmente divergen. El resultado es real… aunque el mecanismo sea distinto.
Lo mismo ocurre con estas sumas. Métodos como la sumación de Cesàro, la regularización de Abel o la zeta-regularización permiten asignarles valores útiles. Son extensiones del lenguaje matemático que no contradicen la aritmética: la amplían.
Y si truncamos la serie tras N términos, la suma crece como ~N²/2. El –1/12 es, en cierto modo, el término constante que queda al restar la divergencia de fondo, como hacen los físicos en teorías de campos.
🧠 Conclusión: una paradoja controlada
El valor –1/12 no es un error ni una trampa. Es un ejemplo brillante de cómo las matemáticas pueden asignar significado incluso a lo que parece absurdo… y cómo ese significado puede tener consecuencias reales para entender el universo.
Esta famosa igualdad no es una suma común. Es una muestra del poder del pensamiento abstracto: una forma de domar lo infinito para hacerlo útil.