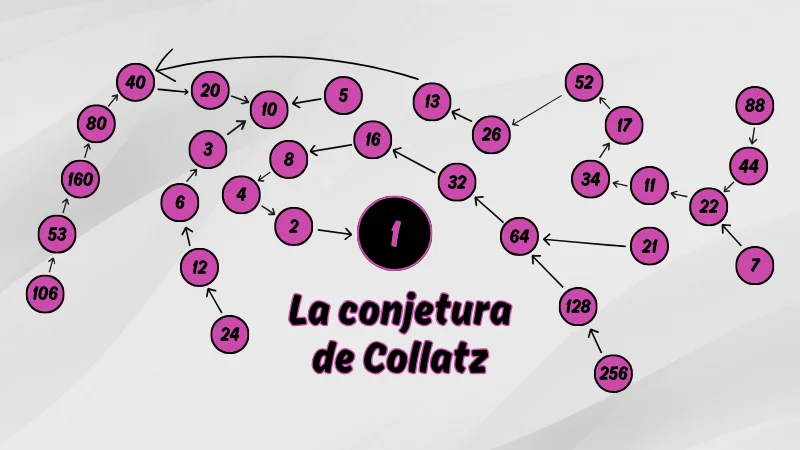
Algunas preguntas en matemáticas parecen complejas y requieren fórmulas sofisticadas. Otras son tan simples que cualquier niño podría entenderlas… y aun así nadie ha logrado resolverlas. La conjetura de Collatz pertenece a este segundo grupo: un problema tan fácil de enunciar que puedes probarlo en casa con papel y lápiz, pero que sigue desafiando a los matemáticos desde 1937.
¿En qué consiste la conjetura?
La regla es sencilla:
-
Toma cualquier número entero positivo
-
Si es par, divídelo entre 2
-
Si es impar, multiplícalo por 3 y súmale 1
-
Repite el proceso con el nuevo número
Ejemplo con el número 6:
6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
Una vez en 1, la secuencia entra en el ciclo 4 → 2 → 1 infinitamente.
El misterio
La conjetura afirma que, sin importar el número inicial, siempre se llegará a 1. Parece cierta: se ha verificado para todos los números hasta 2⁶⁸ (≈ 3×10²⁰). Pero nadie ha podido demostrarlo matemáticamente.
¿Por qué es tan difícil?
Las secuencias pueden crecer de forma impredecible antes de colapsar a 1. El ejemplo más famoso es el 27:
-
Alcanza el valor 9.232 en su punto máximo
-
Tarda 111 pasos en llegar a 1
-
La alternancia entre operaciones lineales (n/2) y no lineales (3n+1) crea un sistema dinámico de comportamiento caótico
Importancia matemática
Collatz no es solo una curiosidad. Se relaciona con:
-
Teoría de sistemas dinámicos discretos
-
Problemas de parada en computación (¿cómo predecir si un algoritmo simple termina?)
-
Teoría de números computacional
El matemático Paul Erdős lo resumió: «Las matemáticas aún no están listas para problemas como éste.»
Conclusión
La conjetura de Collatz nos recuerda que la simplicidad puede esconder una profundidad insondable. Un problema que cualquiera puede entender, pero que nadie puede resolver… por ahora.