¿Sabías que hay números tan grandes que ni con todos los átomos del universo podríamos escribirlos? Uno de ellos, quizás el más famoso, es el número de Graham: tan descomunal que su mera definición escapa a toda intuición… y a toda posibilidad física de representación.
¿De dónde sale el número de Graham?
No es un número arbitrario, ni una extravagancia matemática sin propósito. Aparece en un problema real de combinatoria dentro de la teoría de Ramsey, una rama de las matemáticas que estudia cuándo es inevitable que surjan patrones en estructuras muy grandes.
El matemático Ronald Graham trabajaba con hipercubos n-dimensionales (una generalización del cubo en más de 3 dimensiones). En concreto, buscaba una cota para la dimensión mínima necesaria para garantizar que, al colorear las aristas con dos colores, apareciera un subgrafo plano monocromático (es decir, un conjunto de vértices cuyas conexiones de un solo color formen una figura plana).
Esa dimensión existe… pero es enorme. Y para acotarla por arriba, Graham definió una secuencia de números que crece a una velocidad que desafía cualquier escala convencional.
¿Cómo es de grande?
El número de Graham es el último término de esta secuencia:
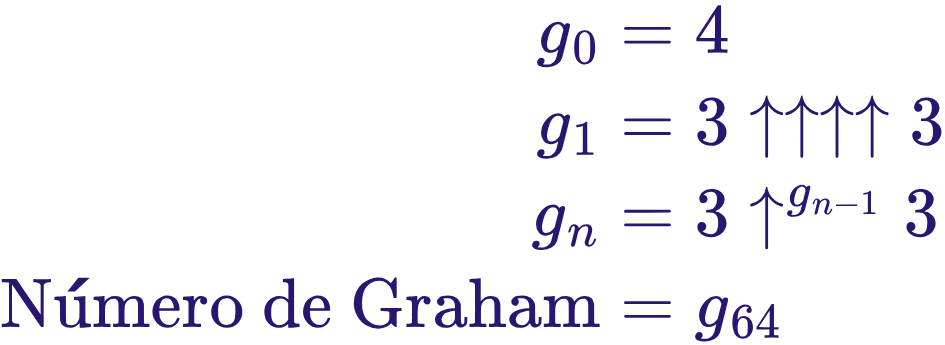
Dónde ↑n representa la notación de flechas de Knuth, una forma de escribir hiperoperaciones (más allá de sumas, multiplicaciones o potencias).
¿Cómo funciona esta notación?
Para entender su velocidad de crecimiento, mira estos ejemplos:

Pero g1 es solo el primer escalón.
g2 = 3 ↑g1 3 ya es absolutamente inimaginable.
Y g64 es una iteración tan brutal que colapsa cualquier analogía física o cosmológica. Cada nuevo término no solo es mayor: es inconcebiblemente mayor que el anterior.
📌 Dato técnico: Se estima que el número de dígitos de Graham es mayor que 1070. Si cada átomo del universo almacenara un dígito, necesitaríamos al menos 1070 universos para escribirlo entero.
¿Y es útil?
Sorprendentemente, sí. El número de Graham es una cota superior demostrada para el problema de coloración de hipercubos. No es la solución exacta (de hecho, la cota real es mucho menor), pero sabemos con certeza que el número buscado está por debajo de G.
Además, aunque no podemos conocer sus cifras… sí sabemos que el último dígito del número de Graham es 7. Esto se puede demostrar gracias a propiedades de la aritmética modular. Es una de las pocas cosas que podemos afirmar sobre él con certeza.
¿Qué nos enseña esto?
El número de Graham no es solo una rareza. Es una lección sobre cómo las matemáticas permiten construir ideas más grandes que cualquier realidad física imaginable.
Nos muestra que hay problemas reales que requieren pensar fuera de escala. Y que existen límites —no de las matemáticas— sino de nuestra capacidad humana de visualizar, escribir o representar ciertos números.
Escala comparativa (con números reales e imaginarios)
| Magnitud | Valor aprox. |
|---|---|
| Número de Avogadro | 6 × 1023 |
| Átomos en el universo observable | 1080 |
| Googol | 10100 |
| Googolplex | 1010100 |
| g1 = 3 ↑↑↑↑ 3 | Ya mayor que un googolplex |
| g64 = Número de Graham | Inescribible en cualquier sistema físico |
Conclusión
Aunque inaccesible físicamente, el número de Graham es perfectamente válido matemáticamente. Su existencia demuestra que la mente humana —y la lógica— pueden operar más allá de los límites del espacio, del tiempo… y de la materia.
“Si el universo es información”, como decía el físico John Archibald Wheeler, “entonces el número de Graham es la prueba de que existen patrones lógicos más vastos que el cosmos mismo.”