¿Qué es el número e?
El número e es una constante matemática que surge de forma natural en problemas de crecimiento exponencial y procesos continuos. Su definición más clásica proviene de un límite:
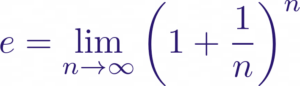
Esta fórmula describe cómo e aparece al calcular el crecimiento compuesto continuo, un concepto fundamental en economía y finanzas.
Además, e puede definirse como la base del logaritmo natural, ln(x), que es la inversa de la función exponencial ex. En términos simples, e es el único número cuya función exponencial tiene una pendiente igual al valor de la función en cada punto.
Origen histórico de e
El número e fue descubierto de forma implícita por matemáticos como John Napier, que desarrolló los logaritmos, y Jakob Bernoulli, quien lo encontró al estudiar el crecimiento compuesto en finanzas. Sin embargo, fue Leonhard Euler quien formalizó e y exploró sus propiedades en el siglo XVIII. Euler no solo dio nombre a e, sino que también demostró su conexión con otros campos de las matemáticas y con las constantes π e i a través de la célebre identidad de Euler:
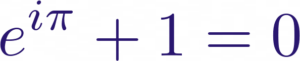
Esta ecuación es considerada por muchos como la fórmula más hermosa de las matemáticas, ya que conecta cinco de las constantes fundamentales: e, π, i, 1 y 0.
Propiedades fundamentales de e
El número e posee propiedades únicas que lo convierten en una herramienta poderosa:
- Derivada de la función exponencial: La función ex es la única que es igual a su propia derivada y a su integral. Matemáticamente:

- Aparición en series infinitas: e se puede expresar como una serie infinita:
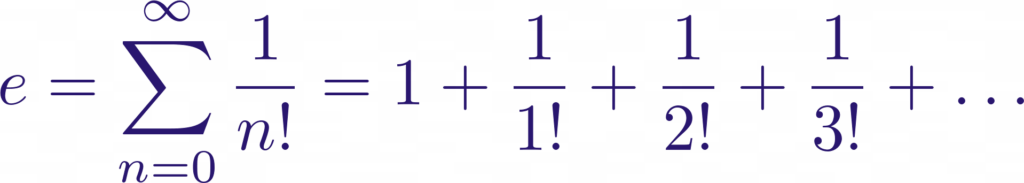
- Número irracional y trascendental: e no puede expresarse como una fracción exacta y, además, no es raíz de ninguna ecuación algebraica con coeficientes racionales, lo que lo convierte en trascendental.
Aplicaciones de e en el mundo real
- Cálculo y modelos matemáticos
La conexión de e con el cálculo diferencial e integral lo hace indispensable para modelar fenómenos de cambio continuo, como el crecimiento poblacional, la desintegración radiactiva o la propagación de enfermedades.
Por ejemplo, el crecimiento poblacional continuo se modela como:

Donde P(t) es la población en el tiempo t, P0 es la población inicial y k es la tasa de crecimiento.
- Economía y finanzas
En economía, e aparece en el cálculo del interés compuesto continuo, una de las formas más precisas de medir el crecimiento del capital. La fórmula es:

Donde A es el monto final, P es el capital inicial, r es la tasa de interés y t es el tiempo.
- Probabilidades y estadística
La probabilidad de eventos raros también involucra e. Un ejemplo clásico es el problema de los cumpleaños: la probabilidad de que un evento no ocurra en absoluto tiende a e-1 cuando los intentos se multiplican infinitamente.
Además, e es fundamental en la distribución exponencial y en el modelo de Poisson, utilizado para describir eventos como el número de llamadas telefónicas recibidas en un centro de atención.
- Biología y ciencias naturales
En biología, e se utiliza para describir procesos como el crecimiento de poblaciones bacterianas y la difusión de sustancias en fluidos. Además, en bioquímica, los modelos de cinética enzimática como la ecuación de Michaelis-Menten están relacionados con esta constante.
- Ingeniería y tecnología
El número e es esencial en el análisis de señales y sistemas, particularmente en el estudio de fenómenos oscilatorios y exponenciales en circuitos eléctricos y telecomunicaciones.
Curiosidades matemáticas de e
- La paradoja de la escalera: En un intento por calcular el interés compuesto continuo, Jakob Bernoulli descubrió e mientras buscaba optimizar el crecimiento de una inversión a intervalos infinitesimales.
- Aparición en el caos: e está relacionado con la entropía en sistemas caóticos y el análisis de la información.
Conclusión
El número e es mucho más que una constante matemática: es un puente que conecta el mundo abstracto de las matemáticas con la realidad física, biológica y económica. Desde describir el crecimiento de una bacteria hasta modelar sistemas financieros complejos, e demuestra que las matemáticas no solo son una ciencia pura, sino una herramienta para entender y cambiar el mundo.