La mecánica celeste, una rama de la física dedicada al estudio del movimiento de los cuerpos celestes, ha sido durante siglos un campo de investigación fascinante. Uno de los problemas más desafiantes que ha cautivado a matemáticos y físicos es el llamado «Problema de los Tres Cuerpos». En esencia, este problema se centra en predecir el movimiento de tres objetos masivos bajo la influencia de la gravedad, teniendo en cuenta las interacciones mutuas entre ellos. A pesar de su aparente simplicidad, este problema es un verdadero quebradero de cabeza que ha desconcertado a científicos durante siglos.
Los Fundamentos del Problema
El Problema de los Tres Cuerpos se plantea de la siguiente manera: Imagina tres cuerpos en el espacio, cada uno de ellos afectado por la gravedad de los otros dos. El objetivo es determinar las trayectorias precisas de estos cuerpos a lo largo del tiempo. A primera vista, esto puede parecer una tarea relativamente sencilla, ya que la Ley de Gravitación Universal de Newton proporciona una fórmula para calcular la atracción gravitatoria entre dos cuerpos. Sin embargo, cuando se agregan más cuerpos, la complejidad se dispara.
La Complejidad Inherentemente Caótica
Una de las características más intrigantes del Problema de los Tres Cuerpos es su naturaleza caótica. En este contexto, el término «caótico» no significa necesariamente desordenado, sino que se refiere a la extrema sensibilidad a las condiciones iniciales. Pequeñas diferencias en las posiciones o velocidades iniciales de los cuerpos pueden llevar a trayectorias completamente diferentes en el futuro.
Este comportamiento caótico se conoce como el «Efecto Mariposa», una metáfora que sugiere que el aleteo de una mariposa en Brasil podría desencadenar un tornado en Texas. En otras palabras, el más mínimo cambio en las condiciones iniciales puede tener un impacto dramático en el comportamiento a largo plazo de un sistema de tres cuerpos.
Historia de Desafíos y Descubrimientos
El Problema de los Tres Cuerpos ha sido una fuente constante de desafíos y descubrimientos en la historia de la física y las matemáticas. Uno de los primeros intentos notables de resolverlo fue realizado por el matemático francés Henri Poincaré a fines del siglo XIX. Poincaré demostró que, en general, el sistema de tres cuerpos no es completamente predecible a largo plazo debido a su naturaleza caótica.
Este resultado fue revolucionario y sentó las bases para la teoría del caos, que ha tenido un impacto significativo en campos que van desde la climatología hasta la biología. Sin embargo, Poincaré también descubrió que hay configuraciones especiales en las que el sistema puede ser estable y predecible, conocidas como «puntos de equilibrio».
Aplicaciones en la Astronomía y la Ciencia
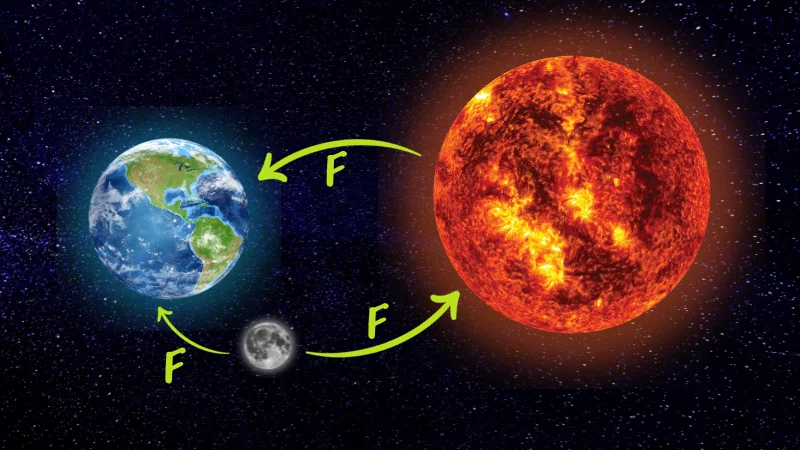
El Problema de los Tres Cuerpos tiene aplicaciones prácticas en la astronomía y la ciencia. Por ejemplo, en el sistema solar, la interacción gravitatoria de la Tierra, la Luna y el Sol representa un caso simplificado de este problema. Comprender estas interacciones es crucial para predecir los movimientos de los cuerpos celestes y planificar misiones espaciales.
Novedades Revolucionarias
Recientemente, un equipo internacional de investigadores anunció un avance extraordinario: el hallazgo de un total de 12.392 nuevas soluciones al Problema de los Tres Cuerpos. Esto representa un aumento exponencial en el número de soluciones halladas en comparación con años anteriores. Antes de 2013, el número de soluciones a este problema de 300 años de antigüedad podía contarse con los dedos de una mano.
Este nuevo estudio se basa en investigaciones anteriores y utiliza una versión mejorada de la técnica que se empleó en el avance más reciente. Aunque los detalles de la investigación aún deben ser revisados por otros expertos antes de ser publicados en una revista, se puede consultar una versión preliminar del estudio.
Las soluciones propuestas tienen una estructura común. Parten de un estado estacionario (sin movimiento). Luego, la atracción gravitatoria los pone en marcha antes de alejarlos entre sí hasta un punto nuevamente estacionario. A partir de ahí, el movimiento se repite en sentido inverso. Esto hace que esas órbitas sean estables, pero sus trazos no son semejantes a los que tendemos a imaginar.
Conclusión
El Problema de los Tres Cuerpos sigue siendo un recordatorio fascinante de la complejidad inherente del universo y de la profunda interconexión entre la física, las matemáticas y la ciencia computacional. A pesar de su aparente simplicidad, este enigma ha desconcertado a algunos de los mejores cerebros de la historia. Su naturaleza caótica y sus aplicaciones prácticas lo convierten en un tema de estudio apasionante que continúa desafiando y estimulando a científicos e investigadores en la actualidad. Con las nuevas soluciones, este problema se convierte en un territorio de descubrimiento aún más vasto, prometiendo desvelar más secretos del cosmos en el futuro.