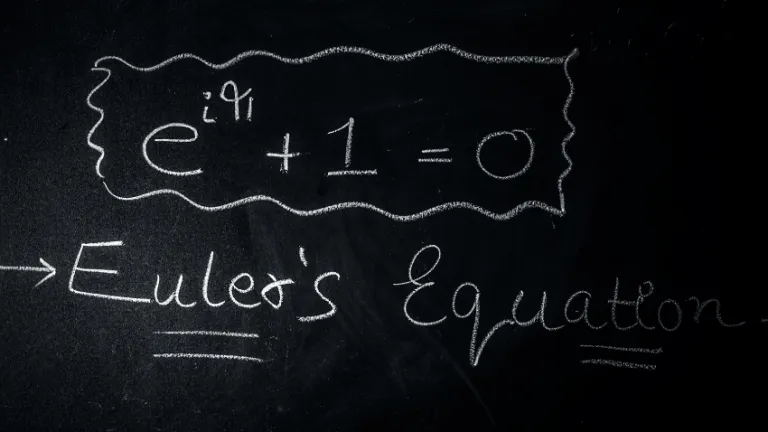Los matemáticos son un grupo extraño. Se decía que Isaac Newton era desagradable, reservado y resentido, mientras que Carl Friedrich Gauss, según varias biografías, era frío y austero, más propenso a criticar que a elogiar. Con frecuencia se afirma que un gran número de matemáticos exhibe signos de autismo y tienen dificultades significativas con la interacción social y la comunicación cotidiana.
Es cierto que algunos de los más grandes se ajustan a este estereotipo, pero el incomparable Leonhard Euler es un contraejemplo. Sus contemporáneos lo describieron como un hombre generoso, amable y cariñoso que mantuvo su carácter bondadoso incluso después de quedar completamente ciego. Esta es una prueba reconfortante de que una personalidad neurótica no es esencial para la destreza matemática.
Leonhard Euler (1707-1783)
Euler, nacido en Basilea en 1707, mostró tempranos signos de genialidad. Estudió con Johann Bernoulli, una de las estrellas de una dinastía de brillantes matemáticos suizos. Euler aprendió mucho de él y pronto eclipsaría a su brillante mentor. Con pocas posibilidades de conseguir un puesto en Suiza, Euler aceptó un puesto en la Academia Imperial de San Petersburgo. Durante una estadía de catorce años, logró muchos avances innovadores en matemáticas y mecánica. También perdió la vista de su ojo derecho.
Estancia en Potsdam
En 1741, cuando las condiciones políticas en Rusia se volvieron amenazadoras, Euler aceptó una invitación de Federico el Grande, rey de Prusia, para trasladarse a la Real Academia de Berlín. Su trabajo allí resultó en la elección para la Royal Society (Londres) y la Academia de París. El rey Federico estaba más interesado en las aplicaciones militares de la ciencia, y Euler tuvo que realizar estudios en balística, navegación, diseño de canales y otras tareas prácticas.
Habiendo perdido el favor del rey, Euler regresó a San Petersburgo en 1766. Su pérdida total de la vista no pareció frenar su producción y continuó produciendo una obra de gran originalidad e ingenio hasta su muerte diecisiete años después.
Euler tenía una memoria fenomenal. En su juventud, aprendió todo el texto de la Eneida de Virgilio y pudo recitarlo sin problemas hasta la vejez. Conocía los primeros cien números primos y también sus cuadrados, cubos y potencias hasta el sexto grado. Euler también tenía una capacidad notable para cálculos mentales complicados. Un biógrafo escribió que Euler calculó sin esfuerzo, “como los hombres respiran, como las águilas se sostienen en el aire”.
Un matemático prolífico
El vasto cuerpo de matemáticas le debe más a Leonhard Euler que a cualquier otra persona. Sus logros cubren un rango enorme y son la base de todas las ramas principales de las matemáticas. En 1911, los estudiosos comenzaron a publicar sus obras completas. Su Opera Omnia incluye unos 900 artículos, muchos de gran profundidad, escritos en alemán, francés y latín. Con 80 volúmenes hasta el momento, este proyecto está a punto de completarse.
Euler revolucionó las matemáticas, ampliando enormemente sus fronteras. Era inagotable, ningún otro matemático ha sido tan prolífico. Su trabajo abarca el cálculo, la geometría diferencial, la teoría de números y las series infinitas. En física, hizo importantes contribuciones a la mecánica analítica y la hidrodinámica. Él sentó las bases de varias nuevas ramas de las matemáticas: teoría de grafos, cálculo de variaciones y ecuaciones diferenciales parciales.
Muchos resultados atribuidos a otros matemáticos se encuentran en las obras de Euler. Tuvo una gran influencia en las matemáticas durante el siglo XIX y continúa inspirando a los matemáticos en la actualidad. Sus libros de texto se mantuvieron como fuentes esenciales durante un siglo o más.
Euler murió repentinamente en 1783. Aunque para entonces estaba completamente ciego, había seguido produciendo nuevos y sorprendentes resultados. La preparación para la publicación de un trabajo atrasado mantuvo ocupados a sus asistentes durante cuatro décadas más.
Fuente: ThatsMaths