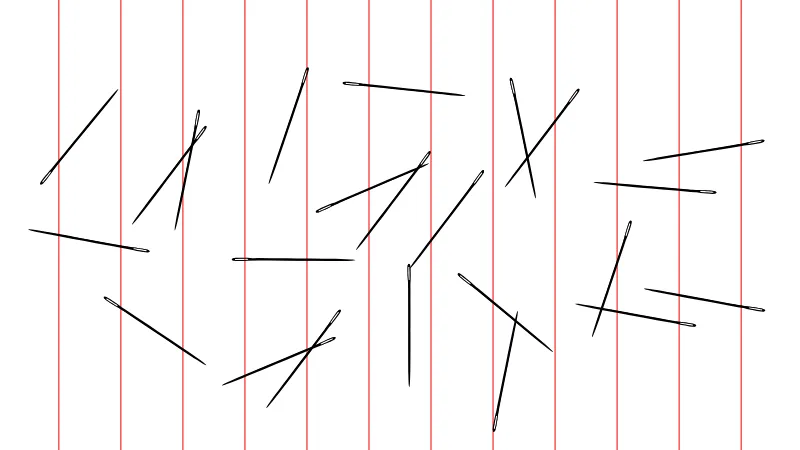La Aguja de Buffon es uno de los experimentos más interesantes y accesibles en el campo de la probabilidad geométrica. Formulado en el siglo XVIII por el matemático francés Georges-Louis Leclerc, también conocido como el Conde de Buffon, este experimento permite aproximar el valor de π utilizando principios básicos de probabilidad y geometría. A través de un procedimiento tan simple como lanzar una aguja sobre una superficie rayada, Buffon logró conectar el mundo de la aleatoriedad con el valor de una de las constantes matemáticas más fundamentales.
El planteamiento del problema
El problema de Buffon se define de la siguiente manera:
Imaginemos una superficie con líneas paralelas separadas por una distancia constante 𝑑. Si lanzamos una aguja de longitud 𝐿, ¿cuál es la probabilidad de que la aguja cruce una de esas líneas al caer? Aunque la respuesta parece depender solo de la geometría, sorprendentemente, el valor de π juega un papel fundamental en esta probabilidad.
Condiciones del Problema
- La longitud de la aguja (𝐿) debe ser menor o igual que la distancia entre las líneas (𝑑).
- La aguja se lanza de forma completamente aleatoria y puede orientarse en cualquier dirección sobre la superficie.
El cálculo de la probabilidad
Cuando se realiza el experimento y se cuenta cuántas veces la aguja cruza una línea, la probabilidad de que ocurra este cruce puede expresarse mediante una fórmula que involucra el número π. La probabilidad de que la aguja cruce una línea es:
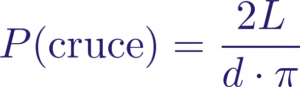
De esta forma, si conocemos el número de lanzamientos y cuántas veces la aguja cruza las líneas, podemos despejar el valor de π y aproximarlo.
Aproximación de π mediante la Aguja de Buffon
Para aproximar π, basta con realizar un gran número de lanzamientos y contar cuántas veces la aguja cruza las líneas. Luego, usando la relación mencionada, podemos obtener una estimación de π mediante la fórmula:
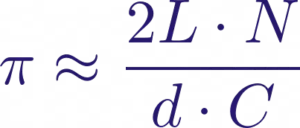
donde:
𝑁 es el número total de lanzamientos, 𝐶 es el número de veces que la aguja cruza una línea.
Conforme el número de lanzamientos aumenta, la aproximación de π se vuelve más precisa debido a la Ley de los Grandes Números, que indica que a mayor número de lanzamientos, el resultado promedio se acercará al valor real de π.
Ejemplo
Supongamos que lanzamos una aguja de 5 cm de largo (𝐿=5) sobre una superficie con líneas separadas cada 10 cm (𝑑=10). Realizamos 1000 lanzamientos y observamos que la aguja cruza una línea en 315 ocasiones (𝐶=315).
Usando la fórmula:
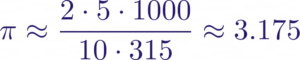
Este valor se acerca bastante al valor real de π (3.14159), y con más lanzamientos podríamos obtener una aproximación aún más precisa.
La Aguja de Buffon y la probabilidad geométrica
La Aguja de Buffon es un ejemplo clásico de probabilidad geométrica, donde las probabilidades dependen de propiedades geométricas, como longitudes y áreas, en lugar de eventos discretos. Este experimento es uno de los primeros ejemplos en los que se usaron métodos probabilísticos para obtener un valor numérico preciso, en este caso, π.
Más allá del experimento: la Aguja de Buffon en la ciencia y la educación
El experimento de la Aguja de Buffon se ha convertido en un recurso popular en la enseñanza de la probabilidad y la estadística, no solo porque permite comprender conceptos abstractos de manera práctica, sino porque también ofrece una forma visual y accesible de estudiar π. Además, algunos algoritmos de simulación utilizan principios similares al experimento de Buffon para calcular probabilidades o resolver problemas complejos en física, biología y ciencias de la computación.
Conclusión
La Aguja de Buffon es un ejemplo fascinante de cómo las matemáticas pueden emerger en situaciones inusuales y aparentemente alejadas de las abstracciones. Aunque el experimento parece simple, en su corazón alberga la capacidad de conectar la geometría, la probabilidad y una de las constantes más importantes de la matemática. Cada lanzamiento de la aguja nos recuerda cómo la ciencia y la matemática nos permiten descubrir conexiones sorprendentes en el mundo que nos rodea.