El número 6174, conocido como la constante de Kaprekar, es un fenómeno matemático fascinante descubierto por el matemático indio D. R. Kaprekar en 1949. Su comportamiento intriga tanto a aficionados como a profesionales, y aunque parece mágico, su explicación radica en propiedades combinatorias y aritméticas. Aquí te explicamos cómo funciona, sus curiosidades y qué se sabe sobre números con más dígitos:
El proceso de Kaprekar (para 4 dígitos)
-
Elige un número de 4 dígitos (no todos iguales, como 1111).
-
Ordena sus dígitos en orden descendente (el número más grande posible).
-
Ordénalos en orden ascendente (el número más pequeño posible, añadiendo ceros si hay dígitos repetidos).
-
Resta el menor al mayor.
-
Repite el proceso con el resultado.
Ejemplo con 2023:
-
Ordenamos sus dígitos de mayor a menor: 3220
-
Ordenamos de menor a mayor: 0223 (conservamos el cero para mantener 4 dígitos)
-
Resta: 3220 – 0223 = 2997
Continuamos el proceso:
-
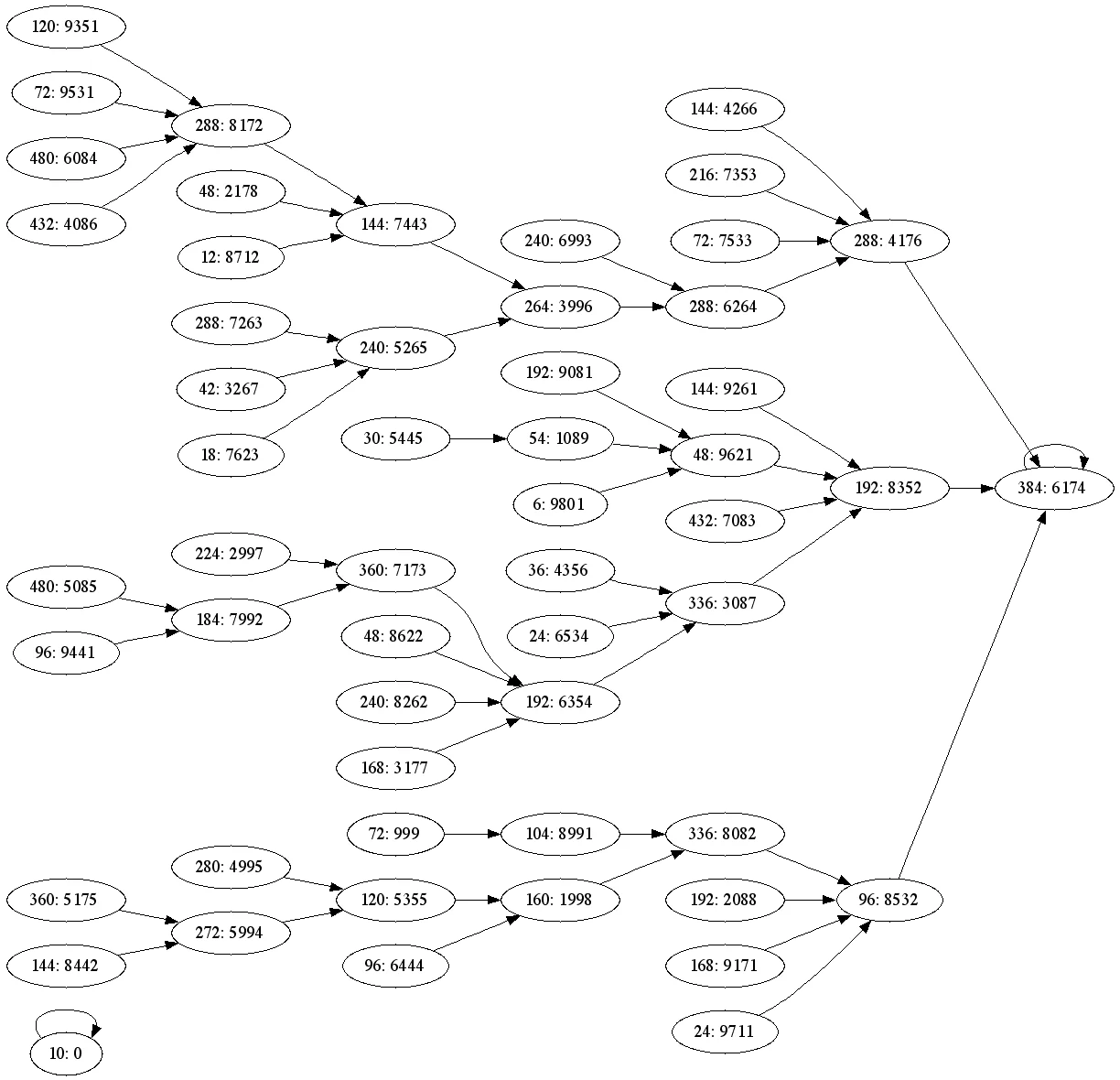
2997 → Mayor: 9972, Menor: 2799 → 9972 – 2799 = 7173
-
7173 → Mayor: 7731, Menor: 1377 → 7731 – 1377 = 6354
-
6354 → Mayor: 6543, Menor: 3456 → 6543 – 3456 = 3087
-
3087 → Mayor: 8730, Menor: 0378 → 8730 – 0378 = 8352
-
8352 → Mayor: 8532, Menor: 2358 → 8532 – 2358 = 6174 (¡la constante!)
En máximo 7 pasos, cualquier número de 4 dígitos no repetitivo llega a 6174 mediante este proceso.
¿Por qué ocurre esto?
La clave está en cómo la resta ordenada reduce sistemáticamente la diferencia entre los números hasta alcanzar un punto fijo. Matemáticamente, el proceso actúa como un atractor: una especie de «hoyo gravitacional» numérico hacia el que caen todas las secuencias.
-
Propiedad combinatoria: Solo hay 10,000 números de 4 dígitos, y el proceso siempre reduce la cantidad de posibilidades.
-
Estabilidad de 6174: Al aplicar el proceso a 6174, se obtiene el mismo número:
-
7641 – 1467 = 6174.
-
¿Y con otros números de dígitos?
-
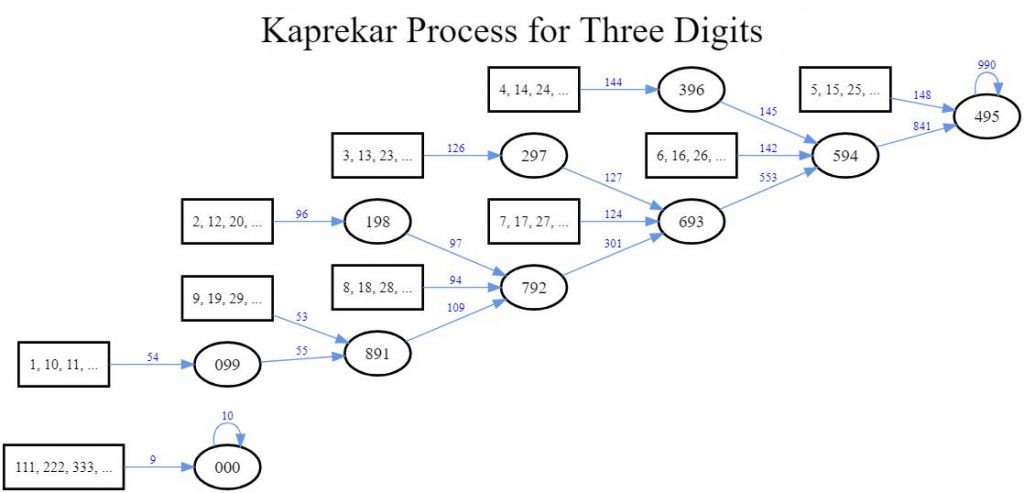
3 dígitos: La constante es 495.
-
Ejemplo: 321 → 321 – 123 = 198 → 981 – 189 = 792 → 972 – 279 = 693 → 963 – 369 = 495.
-
-
2 dígitos: No hay constante, pero sí un ciclo infinito:
-
Ejemplo: 93 → 93 – 39 = 54 → 54 – 45 = 9 → 90 – 09 = 81 → 81 – 18 = 63 → 63 – 36 = 27 → 72 – 27 = 45 → (se repite).
-
-
5 dígitos o más: No hay constantes únicas. Los números entran en ciclos o bucles. Por ejemplo, para 5 dígitos:
-
Algunos números convergen al ciclo 63954 → 61974 → 82962 → 75933 → ….
-
Otros entran en bucles como 74943 → 62964 → 71973 → 83952 → ….
-
¿Por qué solo 3 y 4 dígitos tienen constantes?
Es una pregunta abierta en matemáticas. Se cree que la estructura de las operaciones de Kaprekar en 3 y 4 dígitos permite que el espacio de posibilidades colapse hacia un único número debido a:
-
Simetrías numéricas: La resta elimina gradualmente combinaciones de dígitos.
-
Propiedades modulares: En 4 dígitos, las operaciones «equilibran» los valores hasta estabilizarse.
Para más dígitos, la complejidad aumenta exponencialmente, creando múltiples «sumideros» (ciclos) en lugar de un único punto fijo.
Misterios sin resolver
-
¿Existe una constante para 6 dígitos? Hasta hoy, no se ha encontrado ninguna.
-
¿Por qué los ciclos son tan variados? Dependen de la paridad de los dígitos y su distribución.
-
¿Hay una fórmula general? No. Cada cantidad de dígitos debe estudiarse caso por caso.
¿Por qué es importante?
Aunque parece un simple juego numérico, la constante de Kaprekar ilustra conceptos profundos:
-
Teoría de números: Cómo las operaciones básicas revelan patrones ocultos.
-
Sistemas dinámicos: Comportamiento de atractores y ciclos en iteraciones.
-
Recreación matemática: Muestra que incluso lo aparentemente trivial puede esconder complejidad.
Conclusión
El 6174 es una joya matemática que nos recuerda que, a veces, las preguntas más simples conducen a los misterios más profundos. Como dijo Kaprekar:
«Un número no es grande por sus dígitos, sino por las propiedades que esconde».
¿Te atreves a probar con tu año de nacimiento?





para 5 cifras a mí me dan varias constantes
62964
71973
74943
83952
Le premier calcul est faux! 2997 → 9722 – 2279 = 7443 doit être 2997 → 9972 – 2799 = 7133, puis on obtient 6354, 3087, 8352 6174.
Merci beaucoup pour votre remarque ! 🙏
Vous avez raison, il y avait une petite erreur dans cette étape — c’est maintenant corrigé :
2997 → 9972 − 2799 = 7173, puis la suite mène bien à 6174.
(Et petit clin d’œil : vous avez aussi écrit 7133 au lieu de 7173 😉).
Merci pour votre vigilance ! 👏
Hay que recordar que una vez finalizadas todas las operaciones, si sumamos sus dígitos nos dará como resultado un doble dígito y si siguiendo las instrucciones de la Numerología, si ambos dígitos los reducimos a un solo dígito nos resultará la «grandeza mágica», del dígito 9, que es lo que me ocurre en un libro que he creado, aunque no está editado, llamado: LA GRANDEZA «MÁGICA» DEL DÍGITO 9. GRACIAS.