La paradoja de Monty Hall es un famoso problema de probabilidad que desafía nuestra intuición y tiene implicaciones significativas en la toma de decisiones.
Su nombre proviene del presentador del concurso televisivo estadounidense «Let’s Make a Deal», Monty Hall, y plantea un dilema que, aunque simple en apariencia, esconde una lógica matemática contraintuitiva.
Planteamiento del problema
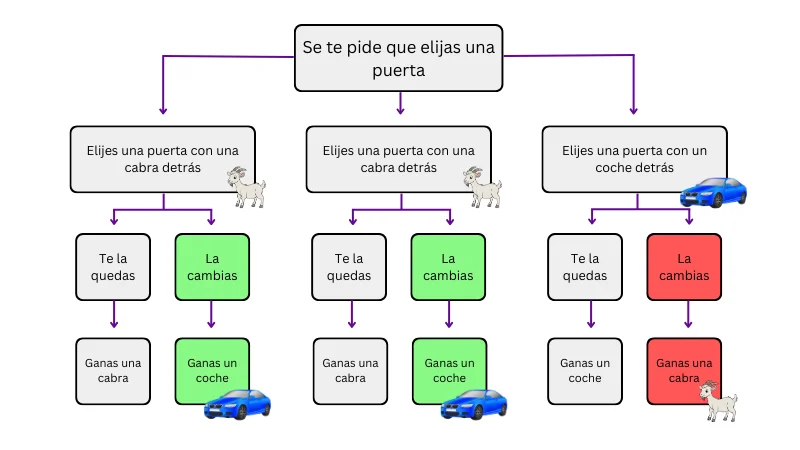
Imagina que participas en un concurso y tienes que elegir entre tres puertas cerradas. Detrás de una hay un coche (el premio), y detrás de las otras dos, cabras. Tú eliges una puerta, por ejemplo, la número 1.
A continuación, el presentador, que conoce perfectamente lo que hay detrás de cada puerta, abre deliberadamente una de las dos puertas que no has elegido, revelando siempre una cabra, y nunca la puerta que esconde el coche. Es importante recalcar que su elección no es aleatoria.
Después de esto, te ofrece la posibilidad de cambiar tu elección inicial por la otra puerta que aún permanece cerrada.
¿Deberías mantener tu elección inicial o cambiar de puerta?
Análisis de probabilidades
A simple vista, podría parecer que, con dos puertas restantes, hay un 50% de probabilidad para cada una. Pero este razonamiento ignora un detalle crucial: el presentador actúa con información perfecta y su decisión influye directamente en las probabilidades. Esto convierte el problema en un caso claro de probabilidad condicional.
Probabilidad de acertar si mantienes tu elección inicial: al principio, tenías 1/3 de probabilidades de elegir la puerta con el coche. Esa probabilidad no cambia.
Probabilidad de acertar si cambias de puerta: hay 2/3 de probabilidad de que el coche estuviera inicialmente en una de las puertas que no elegiste. Como el presentador abre una de ellas y revela una cabra, toda esa probabilidad (2/3) recae ahora sobre la puerta restante.
Cambiar de puerta incrementa tus probabilidades de ganar de 1/3 a 2/3. Es decir, no se duplican literalmente, pero sí aumentan en un 100% respecto a la opción inicial.
Un ejemplo con 100 puertas
Para visualizarlo mejor, imagina que en lugar de tres puertas hay 100. Solo una esconde el coche. Tú eliges, digamos, la número 1. Tu probabilidad de acertar es 1/100.
Ahora, el presentador, que sabe dónde está el coche, abre 98 puertas, todas con cabras. Solo quedan cerradas la puerta que tú elegiste al principio y otra más.
¿Cambiarías?
La lógica es más evidente aquí: la puerta que no elegiste tiene ahora una probabilidad de 99/100 de esconder el coche.
El presentador ha actuado como un filtro informado, guiándote de forma indirecta hacia la puerta correcta.
Un debate histórico
En 1990, esta paradoja se volvió famosa cuando la columnista Marilyn vos Savant la publicó en su sección de la revista Parade. Su solución (recomendar cambiar de puerta) fue tan polémica que recibió miles de cartas, muchas de ellas firmadas por doctores, matemáticos y profesores, asegurando que estaba equivocada.
Con el tiempo, sin embargo, se demostró que tenía razón, lo que subraya cuán contraintuitivo puede resultar el razonamiento probabilístico.
Aplicaciones en la vida real
El problema de Monty Hall no es solo un curioso ejercicio mental; tiene implicaciones prácticas:
Medicina
En pruebas para enfermedades raras, un resultado positivo no siempre significa que realmente estás enfermo.
Por ejemplo, si una enfermedad tiene una prevalencia del 1% y la prueba no es perfecta, la mayoría de los positivos pueden ser falsos positivos, porque la información previa (baja prevalencia) condiciona el resultado.
Negocios
Al lanzar un producto al mercado, es común hacer pruebas y eliminar opciones que no funcionan.
Ese proceso actúa como el presentador eliminando cabras. En este contexto, cambiar la estrategia inicial tras recopilar nueva información puede aumentar las probabilidades de éxito.
¿Y si lo pruebas tú mismo?
¿Aún no te convence? Haz el experimento con otra persona. Usad tres cartas: dos reinas (las cabras) y un as (el coche). Uno de vosotros será el presentador (que conoce la ubicación del as) y el otro, el concursante. El concursante elige una carta. El presentador, sabiendo qué hay en cada una, debe descartar una de las dos cartas no elegidas, mostrando siempre una reina. Ahora el concursante decide: ¿se queda con su carta o cambia a la otra? Repetid la prueba unas 20 veces y llevad la cuenta de los aciertos en cada estrategia. Veréis cómo cambiar gana casi dos de cada tres veces. ¡La estadística no miente!
Conclusión
La paradoja de Monty Hall nos recuerda lo difícil que puede ser razonar correctamente en situaciones de incertidumbre. Nos invita a cuestionar nuestras intuiciones, entender las probabilidades condicionales y aplicar el pensamiento lógico para tomar mejores decisiones, tanto en contextos matemáticos como en la vida diaria.