¿Cuántas personas crees que se necesitan en una sala para que dos de ellas cumplan años el mismo día?
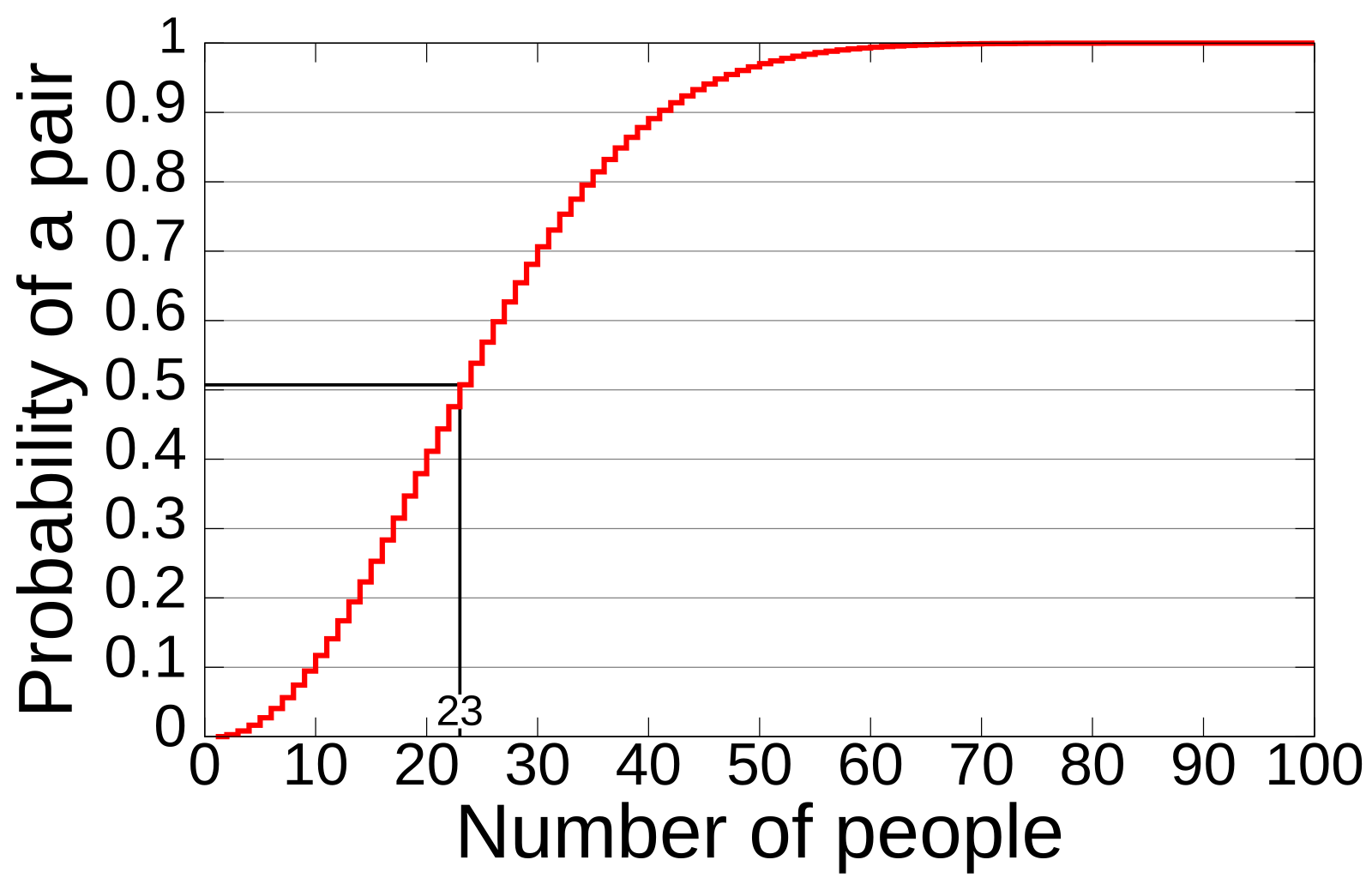
La intuición nos dice que deberían ser muchas, tal vez 100 o más… pero la realidad matemática es muy distinta: con solo 23 personas, la probabilidad de coincidencia ya supera el 50%.
Esto es lo que conocemos como la paradoja del cumpleaños.
¿Por qué es una paradoja?
Porque desafía la intuición. Solemos pensar en nuestra probabilidad personal de coincidir con otra persona (1 entre 365, si ignoramos los años bisiestos).
Pero el truco está en que no se trata de tu cumpleaños contra los demás, sino de todas las posibles parejas dentro del grupo.
A medida que el grupo crece, el número de comparaciones posibles crece mucho más rápido de lo que pensamos.
De hecho, el número de pares en un grupo de nn personas es:

Para , esto da 253 pares posibles, lo que hace la coincidencia mucho más probable de lo que nuestra intuición sugiere.
El cálculo detrás del resultado
La forma más sencilla de calcularlo es pensar en la probabilidad contraria: que no haya coincidencias.

y por tanto:
![]()
Resultados concretos y contundentes
-
23 personas: probabilidad de coincidencia >50% (50,73%).
-
30 personas: probabilidad ≈ 70,6%.
-
50 personas: probabilidad >97% (97,04%).
-
70 personas: probabilidad ≈ 99,9% (99,916%).
Nota: estos cálculos se hacen ignorando los años bisiestos. Si se incluye el 29 de febrero, las probabilidades se reducen muy ligeramente (por ejemplo, con 23 personas baja a 50,63%), pero el efecto es mínimo y no cambia las conclusiones.
Más sorprendente todavía
Lo realmente contraintuitivo es la rapidez con la que crece la probabilidad:
-
Con 23 personas, más de la mitad de las veces habrá coincidencia.
-
Con 50, se eleva al 97%.
-
Con 70, llega al 99,9%: prácticamente seguro.
Aplicaciones reales
La paradoja del cumpleaños no es solo una curiosidad:
En criptografía
Explica el llamado “ataque del cumpleaños”: para una función hash con NN posibles salidas, se necesitan solo alrededor de √N intentos para encontrar una colisión con alta probabilidad, en lugar de NN.
-
Ejemplo: un hash de 128 bits tiene N = 2128 posibles resultados.
Con la paradoja del cumpleaños, una colisión puede encontrarse en unas 264 operaciones. -
Por esto, protocolos modernos utilizan hashes más largos como SHA-256, cuya seguridad efectiva frente a colisiones es de unas 2128 operaciones.
El ataque del cumpleaños no es una rareza teórica: es una amenaza real que condiciona el diseño de la seguridad digital.
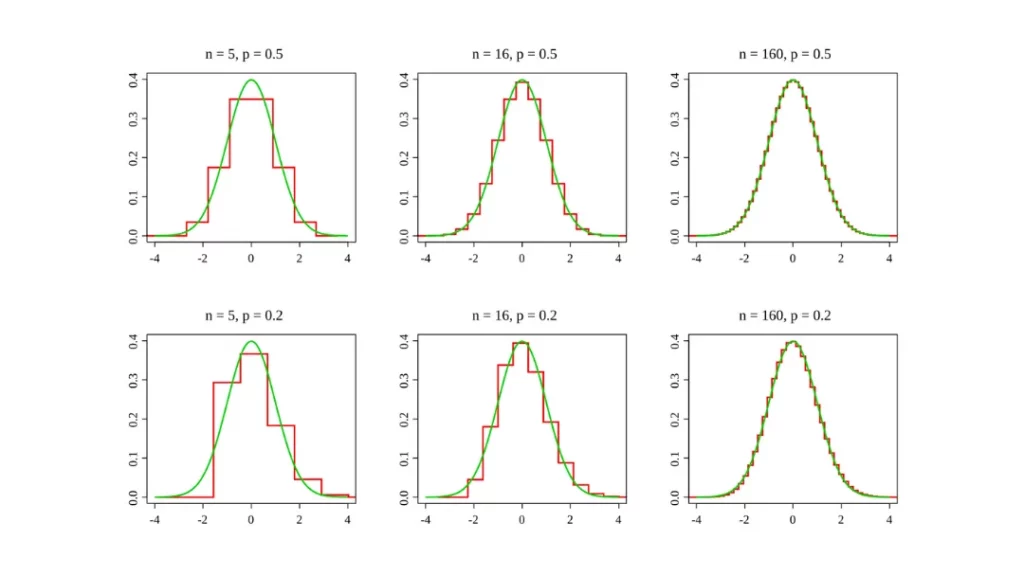
En estadística
La paradoja ayuda a visualizar cómo funcionan las distribuciones de probabilidad en grandes grupos, y cómo los sucesos raros se vuelven frecuentes cuando hay suficientes comparaciones posibles.
En la vida cotidiana
Puedes comprobarlo con un sencillo “experimento social”: en una reunión con más de 30 personas, apuesta a que al menos dos comparten cumpleaños.
Las matemáticas estarán de tu lado.
Y no es solo teoría: en el Mundial de Fútbol de 2014, 17 de los 32 equipos (más del 50%) tenían al menos dos jugadores que cumplían años el mismo día. ¡La paradoja en acción!
Conclusión
La paradoja del cumpleaños nos enseña que el azar puede ser engañoso.
Aunque cada persona tenga solo una probabilidad de 1/365 de coincidir con otra, el número de pares posibles crece de forma cuadrática con el tamaño del grupo.
El resultado: coincidencias que parecen imposibles se vuelven casi seguras.
Una lección que va más allá de las matemáticas: confiar demasiado en la intuición puede llevarnos a errores.
La próxima vez que te enfrentes a un problema de probabilidad, recuerda la paradoja del cumpleaños… y piensa dos veces antes de apostar.