Si te pidieran analizar una lista de miles de facturas, precios de acciones o la extensión de los ríos del mundo, ¿qué probabilidad creerías que tiene cada número (\(1, 2, \dots, 9\)) de ser el primer dígito de esas cifras?
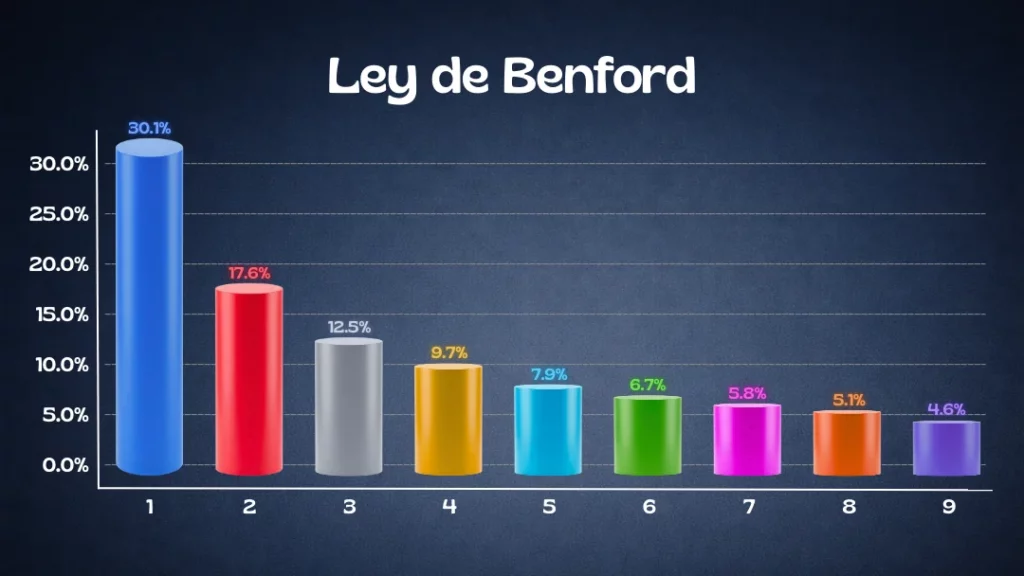
Nuestra intuición nos dice que, al haber nueve dígitos posibles, cada uno debería aparecer aproximadamente el 11,1% de las veces. Sin embargo, la realidad desafía la lógica simple. En los conjuntos de datos que crecen de forma natural, el número \(1\) aparece como primer dígito casi el 30% de las veces, mientras que el \(9\) aparece menos del 5%. Este fenómeno se conoce como la Ley de Benford.
Un descubrimiento por «desgaste»
En 1881, el astrónomo Simon Newcomb notó que las primeras páginas de las tablas de logaritmos estaban mucho más sucias que las últimas. Sus colegas buscaban mucho más a menudo números que empezaban por \(1\) que por \(9\). En 1938, el físico Frank Benford probó esta hipótesis en miles de datos (poblaciones, constantes físicas, áreas de países) y confirmó que el patrón era universal.
La fórmula matemática
La probabilidad de que un número comience con el dígito \(d\) (donde \(d \in {1, 2, \dots, 9}\)) viene dada por la siguiente fórmula:
\(P(d) = \log_{10} \left( 1 + \frac{1}{d} \right)\)
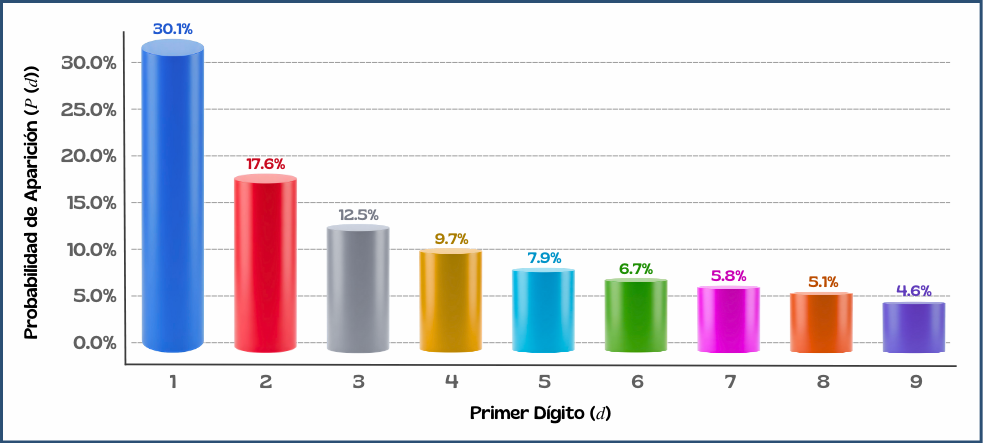
Si aplicamos esta fórmula para cada dígito, obtenemos el contraste visual que gobierna los datos:
| Primer Dígito (\(d\)) | Probabilidad de Aparición (\(P(d)\)) |
| \(1\) | \(30,1%\) |
| \(2\) | \(17,6%\) |
| \(3\) | \(12,5%\) |
| \(4\) | \(9,7%\) |
| \(5\) | \(7,9%\) |
| \(6\) | \(6,7%\) |
| \(7\) | \(5,8%\) |
| \(8\) | \(5,1%\) |
| \(9\) | \(4,6%\) |
¿Por qué ocurre esto?
La explicación reside en la naturaleza logarítmica del crecimiento. Para que una cuenta de \(100\) euros pase a empezar por \(2\), debe crecer un 100% (llegar a \(200\)). Sin embargo, para que una de \(800\) pase a empezar por \(9\), solo necesita crecer un 12,5% (llegar a \(900\)). Los números pasan mucho más tiempo «siendo un uno» que cualquier otro dígito.
A esto se le llama invarianza de escala. Esto significa que la ley funciona igual si medimos la longitud de los ríos en kilómetros, millas o codos: la frecuencia del primer dígito se mantiene constante.
Aplicaciones: El detective de datos
-
Detección de Fraude Fiscal: Los seres humanos, al inventar números, tendemos a distribuirlos de forma uniforme. Si las facturas de una empresa muestran demasiados números empezando por \(5\) o \(6\) y muy pocos por \(1\), Hacienda detectará la anomalía de inmediato.
-
Análisis de Elecciones (con cautela): Se ha propuesto su uso para analizar resultados electorales. Sin embargo, es un método controvertido, ya que la distribución de los votos no siempre cumple los requisitos de Benford; por tanto, una desviación no prueba fraude por sí sola, pero sí señala datos que merecen una auditoría detallada.
-
Fraude Científico: Sirve para validar si los datos de un experimento clínico han sido fabricados. Nuestro cerebro no está cableado para pensar de forma logarítmica, sino lineal, lo que hace casi imposible fabricar datos falsos que pasen este test sin un patrón detectable.
⚠️ ¿Cuándo NO se aplica?
No funciona con conjuntos de datos con límites artificiales o rangos estrechos:
-
Números de teléfono o códigos postales.
-
Estaturas humanas (la mayoría empieza por \(1\)).
-
Precios con límites máximos o mínimos fijos.
La Ley de Benford nos recuerda que el universo tiene un orden matemático subyacente que escapa a nuestra percepción cotidiana, convirtiendo un simple dígito en una prueba de autenticidad.