La mecánica de fluidos, un fascinante campo en la intersección de la física y la ingeniería, nos sumerge en un universo de movimiento y transformación. Desde el diseño de aeronaves hasta el funcionamiento del corazón humano, la mecánica de fluidos desempeña un papel esencial en nuestra comprensión del mundo y en la creación de innovadoras tecnologías.
Conceptos fundamentales
Fluidos en reposo:
- Presión: La fuerza que un fluido ejerce sobre una superficie por unidad de área. Se calcula como la fuerza normal dividida por el área: P=F/A
- Densidad: La masa de un fluido por unidad de volumen. Se calcula como la masa del fluido dividida por el volumen que ocupa: ρ=m/V
- Fuerzas en fluidos en reposo: Peso, fuerza de empuje y presión atmosférica.
Fluidos en movimiento:
- Velocidad: La rapidez con la que se mueve un fluido. Se define como la distancia recorrida por el fluido en un tiempo determinado: v=d/t
- Caudal: La cantidad de fluido que pasa por un punto en un tiempo determinado. Se calcula como el volumen del fluido que pasa dividido por el tiempo: Q=V/t
- Viscosidad: La resistencia de un fluido a fluir. Se define como la fuerza tangencial por unidad de área necesaria para mantener un flujo laminar: μ=τ/γ
- Flujo laminar: Flujo ordenado y suave de un fluido, caracterizado por capas que se deslizan sin mezclarse.
- Flujo turbulento: Flujo caótico y desorganizado de un fluido, caracterizado por remolinos y fluctuaciones de velocidad.
Ecuaciones
- Ecuación de continuidad: La masa que entra en un sistema debe ser igual a la masa que sale: (∂ρ/∂t)+∇⋅(ρv)=0
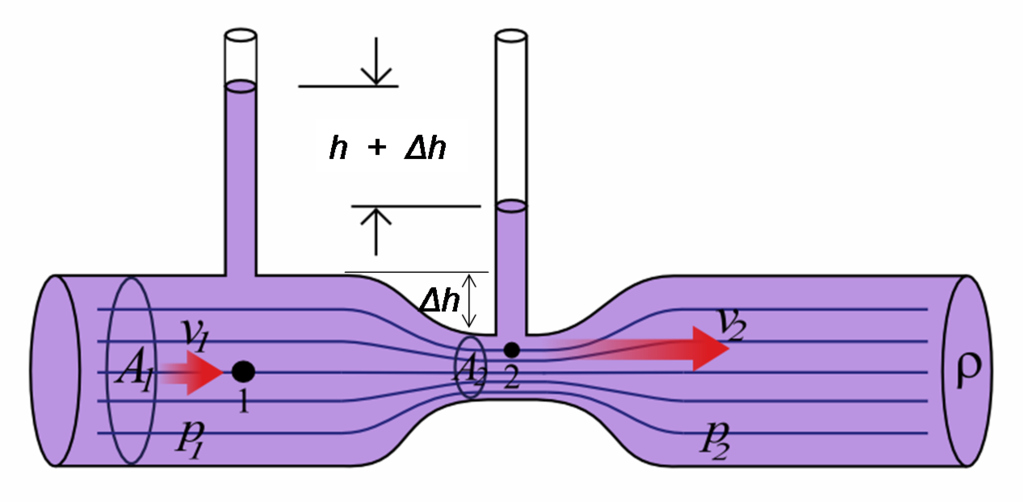
- Ecuación de Bernoulli: Describe la relación entre presión, velocidad y altura en un fluido en movimiento: P+((1/2)ρv2)+ρgh=constante
- Ecuaciones de Navier-Stokes: Conjunto de ecuaciones diferenciales no lineales que describen la conservación de masa, cantidad de movimiento y energía en un fluido en movimiento.
Aplicaciones en ingeniería
Aerodinámica
- Diseño de alas de avión, turbinas eólicas y vehículos de Fórmula 1.
- Optimización de la eficiencia del vuelo y reducción de la resistencia del aire.
Hidrodinámica
- Diseño de barcos, cascos de submarinos y centrales hidroeléctricas.
- Aprovechamiento de la energía del agua y diseño de sistemas de propulsión marina.
Ingeniería civil
- Diseño de puentes, sistemas de riego y plantas de tratamiento de agua.
- Análisis de las fuerzas que actúan sobre las estructuras y diseño de sistemas eficientes para el transporte de agua.
Investigaciones avanzadas
Nanofluidos
- Desarrollo de nanofluidos para aplicaciones médicas, como la administración de medicamentos dirigida.
- Mejora de la eficiencia energética y desarrollo de materiales con propiedades únicas.
Inteligencia artificial
- Implementación de inteligencia artificial para optimizar el diseño de sistemas y prever el comportamiento de los fluidos en condiciones complejas.
- Desarrollo de herramientas de simulación más precisas y eficientes.
Ejemplos de aplicación de fórmulas
Ecuación de flujo de agua a través de una tubería
-
Q: Caudal del agua (m³/s)
-
π: Constante matemática (3.14159)
-
R: Radio de la tubería (m)
-
ΔP: Diferencia de presión entre los extremos de la tubería (Pa)
-
μ: Viscosidad del agua (Pa·s)
-
L: Longitud de la tubería (m)
Ejemplo:
Suponiendo que tenemos una tubería de agua con un radio de 0.05 m, una longitud de 10 m y una diferencia de presión de 1000 Pa. La viscosidad del agua a 20 °C es de 0.001 Pa·s.
Calculando el caudal:
Q = π * (0.05 m)⁴ * 1000 Pa / (8 * 0.001 Pa·s * 10 m) Q ≈ 0.00196 m³/s
Interpretación:
El caudal del agua a través de la tubería es de aproximadamente 0.00196 m³/s, equivalente a 1.96 litros por segundo.
Ecuación de Bernoulli
-
P: Presión del fluido (Pa)
-
ρ: Densidad del fluido (kg/m³)
-
v: Velocidad del fluido (m/s)
-
g: Gravedad (9.81 m/s²)
-
h: Altura del fluido (m)
Ejemplo:
Supongamos que un avión vuela a una velocidad de 100 m/s a una altura de 1000 m. La densidad del aire a esa altura es de 1.225 kg/m³.
Calculando la presión:
P + ½ * 1.225 kg/m³ * (100 m/s)² + 1.225 kg/m³ * 9.81 m/s² * 1000 m = constante
P ≈ 101325 Pa
Interpretación:
La presión del aire en el punto donde se encuentra el avión es de aproximadamente 101325 Pa, equivalente a la presión atmosférica a esa altura.
Ecuación de fuerza de empuje
-
Fe: Fuerza de empuje (N)
-
ρ: Densidad del fluido (kg/m³)
-
V: Volumen del objeto sumergido (m³)
-
g: Gravedad (9.81 m/s²)
Ejemplo:
Supongamos que un objeto con un volumen de 0.1 m³ está sumergido en agua. La densidad del agua es de 1000 kg/m³.
Calculando la fuerza de empuje:
Fe = 1000 kg/m³ * 0.1 m³ * 9.81 m/s² Fe ≈ 981 N
Interpretación:
La fuerza de empuje que actúa sobre el objeto sumergido en agua es de aproximadamente 981 N.
Desafíos futuros y conclusiones
La mecánica de fluidos se encuentra en una posición única para abordar algunos de los desafíos más apremiantes del siglo XXI. A medida que la población mundial continúa creciendo, la demanda de recursos naturales como el agua y la energía también aumenta. La mecánica de fluidos puede desempeñar un papel fundamental en el desarrollo de tecnologías sostenibles que nos permitan satisfacer estas necesidades de manera responsable y eficiente.
Algunos de los desafíos específicos que la mecánica de fluidos puede ayudar a enfrentar incluyen:
- Desarrollo de sistemas de energía eficientes: La mecánica de fluidos puede usarse para diseñar turbinas eólicas más eficientes, centrales hidroeléctricas y otros sistemas de energía renovable.
- Mejora de la gestión del agua: La mecánica de fluidos puede ayudar a desarrollar sistemas de riego más eficientes, reducir las fugas en las redes de agua potable y mejorar la calidad del agua.
- Reducción de la contaminación: La mecánica de fluidos puede usarse para desarrollar tecnologías de limpieza ambiental más efectivas, como filtros de aire y sistemas de tratamiento de aguas residuales.
- Diseño de ciudades sostenibles: La mecánica de fluidos puede ayudar a los urbanistas a diseñar ciudades más eficientes y sostenibles, con mejores sistemas de transporte, edificios más eficientes energéticamente y espacios verdes más accesibles.
Para abordar estos desafíos, la comunidad de mecánica de fluidos necesita continuar investigando y desarrollando nuevas tecnologías. Algunas áreas clave de investigación incluyen:
- Desarrollo de nuevos materiales con propiedades avanzadas: Los nuevos materiales con propiedades como la superhidrofobicidad o la autolimpieza pueden tener un impacto significativo en la eficiencia de los sistemas de fluidos.
- Mejora de las técnicas de modelado y simulación: Las técnicas de modelado y simulación más precisas pueden ayudar a los ingenieros a diseñar sistemas de fluidos más eficientes y optimizar su rendimiento.
- Desarrollo de herramientas de inteligencia artificial: La inteligencia artificial puede usarse para analizar datos de fluidos, predecir el comportamiento de los sistemas de fluidos y optimizar su operación.
Además de los desafíos mencionados anteriormente, la mecánica de fluidos también puede ser utilizada para:
- Desarrollo de prótesis y dispositivos médicos: La mecánica de fluidos puede usarse para diseñar prótesis más eficientes y cómodas, así como dispositivos médicos para el tratamiento de enfermedades cardiovasculares y respiratorias.
- Exploración espacial: La mecánica de fluidos es fundamental para el diseño de naves espaciales y cohetes, así como para el estudio de la atmósfera de otros planetas.
- Mejora de la industria manufacturera: La mecánica de fluidos puede usarse para optimizar los procesos de fabricación, reducir el consumo de energía y mejorar la calidad de los productos.
En conclusión, la mecánica de fluidos es una ciencia poderosa con un enorme potencial para mejorar la calidad de vida en todo el mundo. Al abordar los desafíos del futuro con innovación y creatividad, la comunidad de mecánica de fluidos puede contribuir a la creación de un futuro más sostenible y próspero para todos.