René Descartes (1596-1650) es reconocido como uno de los filósofos más influyentes de la modernidad, pero su contribución a las matemáticas, especialmente a la geometría, es igualmente monumental. Descartes no solo revolucionó el pensamiento filosófico con su famoso «pienso, luego existo», sino que también transformó el modo en que concebimos el espacio y las formas geométricas. Con su obra «La Géométrie» (1637), Descartes dio un giro radical al desarrollo de la geometría, sentando las bases de la geometría analítica que conocemos hoy.
El contexto histórico: Renacimiento y ciencia
Durante el Renacimiento, las matemáticas estaban en un proceso de evolución gracias a avances en la astronomía, la mecánica y la navegación. Figuras como Galileo y Kepler ya habían comenzado a conectar los números con los fenómenos físicos, pero fue Descartes quien unificó las matemáticas y la geometría de una forma revolucionaria. Antes de su tiempo, la geometría se basaba en los métodos desarrollados por Euclides en la antigua Grecia. Este enfoque geométrico clásico utilizaba herramientas como la regla y el compás para estudiar las figuras, pero no había una forma directa de conectar la geometría con el álgebra. Aquí es donde Descartes hizo su mayor contribución.
La geometría analítica: Un nuevo lenguaje matemático
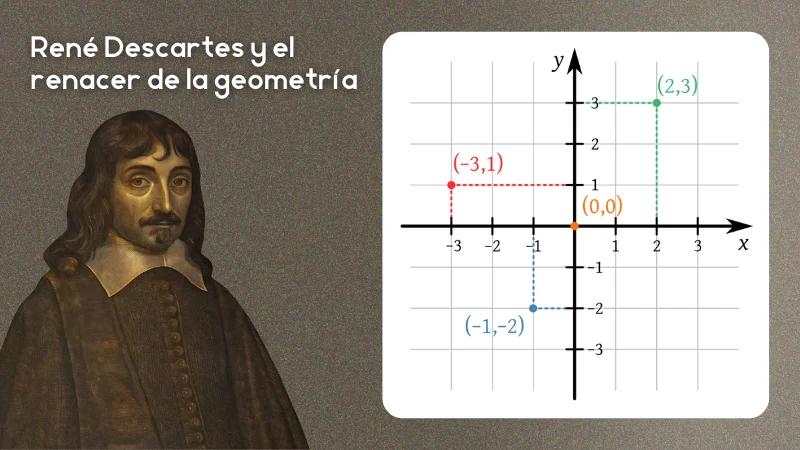
En su obra «La Géométrie», Descartes introdujo un método que hoy consideramos básico: la geometría analítica, una disciplina que utiliza coordenadas numéricas para describir formas geométricas. Este enfoque permitió, por primera vez, traducir los problemas geométricos en ecuaciones algebraicas. El principal avance de Descartes fue la introducción de lo que ahora conocemos como el plano cartesiano. Al usar un sistema de coordenadas, cualquier punto en el plano puede describirse mediante un par de números, lo que permitió representar curvas y figuras geométricas a través de ecuaciones algebraicas. Esta conexión entre el álgebra y la geometría permitió resolver problemas geométricos de una forma mucho más eficiente y clara.
Un cambio paradigmático en el pensamiento matemático
La propuesta de Descartes de fusionar el álgebra y la geometría no fue simplemente una mejora técnica, sino que también representó un cambio fundamental en el modo en que los matemáticos pensaban sobre el espacio. Al usar ecuaciones algebraicas para describir curvas, Descartes permitió que los matemáticos abordaran problemas geométricos abstractos de una manera mucho más flexible y general. Por ejemplo, un círculo, que antes se veía solo como una figura con un centro y un radio, ahora podía describirse mediante una simple ecuación: x² + y² = r². Esto facilitaba el análisis y resolución de problemas que antes requerían construcciones geométricas complejas.
Aplicaciones en la ciencia y la ingeniería
La geometría analítica no solo transformó las matemáticas, sino que también abrió nuevas puertas en la física, la astronomía y la ingeniería. El sistema cartesiano permitió a los científicos de la época, y de generaciones futuras, describir trayectorias, órbitas y fenómenos físicos utilizando ecuaciones matemáticas precisas. El trabajo de Descartes influyó directamente en los avances científicos de figuras como Isaac Newton y Gottfried Wilhelm Leibniz, quienes utilizaron la geometría analítica para desarrollar el cálculo. Este fue un paso crucial para poder describir los movimientos de los planetas, las fuerzas y otras áreas de la física que requerían una conexión precisa entre el espacio y el tiempo.
Hoy en día, la geometría analítica sigue siendo una herramienta fundamental en campos como la ingeniería, la física, la economía y la informática. Por ejemplo, en la visualización de datos, los gráficos cartesianos permiten representar de manera clara y concisa grandes conjuntos de información. Además, en el campo de la inteligencia artificial, la geometría analítica es esencial para el desarrollo de algoritmos de visión por computadora y reconocimiento de patrones.
Descartes: Filósofo y matemático
Lo más sorprendente de la obra de Descartes es cómo su interés filosófico influyó en su trabajo matemático. Para Descartes, la geometría analítica no era simplemente una herramienta útil, sino también una forma de comprender la realidad. Su visión filosófica del mundo, basada en la claridad y la certeza, encontró en las matemáticas un vehículo perfecto para expresar su búsqueda de la verdad. Al igual que en su filosofía, Descartes buscaba simplificar y clarificar el conocimiento humano. Su sistema de coordenadas ofrecía una forma ordenada y comprensible de representar el espacio, algo que resonaba con su deseo de construir un sistema filosófico basado en la razón y la evidencia.
El legado de Descartes en la matemática moderna
Hoy, el impacto de Descartes en la geometría y en las matemáticas en general es incuestionable. La geometría analítica es una parte central de la educación matemática y sigue siendo utilizada en campos tan diversos como la ingeniería, la física, la economía y la informática. El plano cartesiano, en particular, es una herramienta diaria para cualquier estudiante de matemáticas. Desde los cálculos más simples hasta los estudios más avanzados en física teórica o inteligencia artificial, la contribución de Descartes ha dejado una huella imborrable en nuestra forma de entender el mundo.
Si bien Descartes fue pionero en la geometría analítica, es importante destacar que matemáticos como Pierre de Fermat también realizaron contribuciones significativas en este campo. Fermat, por ejemplo, trabajó de forma independiente en el desarrollo de la geometría analítica y llegó a resultados similares a los de Descartes. Sin embargo, fue Descartes quien publicó sus hallazgos de manera más completa y sistemática, lo que le otorgó un mayor reconocimiento.
Conclusión
René Descartes no solo revolucionó la filosofía, sino que también reconfiguró el mundo de las matemáticas con la introducción de la geometría analítica. Su legado trasciende su época, conectando el pensamiento abstracto con aplicaciones prácticas que han influido en el progreso de la ciencia y la tecnología hasta el día de hoy. Su trabajo es una prueba de que las ideas más simples, como la relación entre dos ejes y un punto, pueden tener un impacto profundo y duradero en nuestra comprensión del universo.
