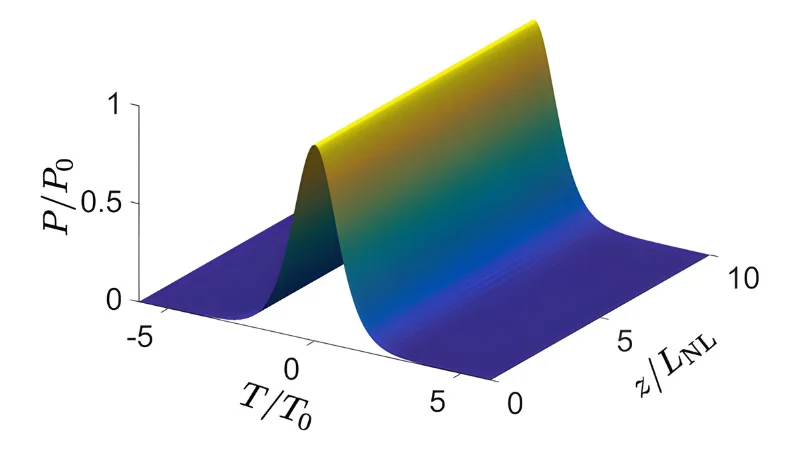
Las ondas suelen dispersarse o disiparse… excepto cuando son solitones. Estas ondas solitarias mantienen su forma y velocidad incluso tras recorrer grandes distancias o interactuar con otras. Descubre cómo funcionan y por qué son clave en física, telecomunicaciones y más.
¿Qué es un solitón?
Un solitón es una onda localizada que no se dispersa gracias a un equilibrio único:
- Dispersión (tendencia a extenderse).
- No linealidad (efecto de «autorefuerzo» que la compacta).
Descubrimiento histórico
En 1834, el ingeniero escocés John Scott Russell observó una onda solitaria en el canal Union (Edimburgo) que viajó 3 km sin deformarse. La llamó «gran ola de traslación», pero la comunidad científica la ignoró hasta 1895, cuando Diederik Korteweg y Gustav de Vries derivaron la ecuación que la describe (KdV):
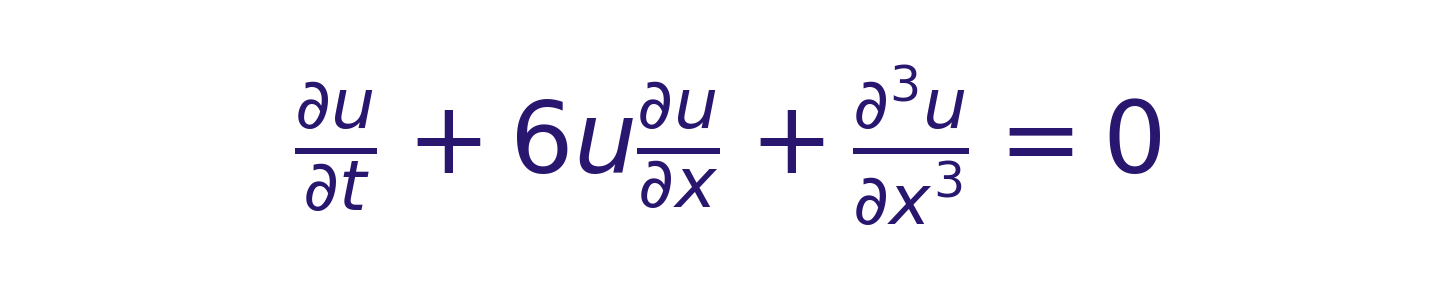
Donde:
- u(x,t): Altura de la onda en posición x y tiempo t.
- Tercer término: Efecto dispersivo (difumina la onda).
- Segundo término: No linealidad (la compacta).
Tipos de solitones
No todos los solitones son iguales. Algunos ejemplos:
- Solitones topológicos: Mantienen su forma debido a propiedades geométricas (ej: kinks en cadenas magnéticas).
- Solitones ópticos: Pulsos de luz en fibras no lineales.
- Solitones de materia: En condensados de Bose-Einstein.
¿Por qué son importantes?
1. Telecomunicaciones revolucionarias
En fibras ópticas, los pulsos de luz normales se dispersan tras ~100 km. Los solitones ópticos solucionan esto:
- Usan la no linealidad de Kerr (índice de refracción dependiente de la intensidad).
- Permiten transmisión de datos transoceánicos sin repetidores (ahorro de costes).
Ejemplo: En 1988, los laboratorios Bell enviaron un solitón a 4,000 km sin pérdidas.
2. Modelado de tsunamis y olas extremas
Algunos tsunamis se comportan como solitones en aguas profundas, manteniendo energía hasta llegar a costa. La ecuación KdV explica por qué olas de 30 m (como las de Indonesia, 2004) pueden viajar miles de km.
3. Física cuántica: Condensados de Bose-Einstein
En gases ultrafríos (~1 µK), los solitones son ondas de materia que no se dispersan. Se usan para estudiar:
- Superfluidez.
- Transiciones de fase cuánticas.
4. Matemáticas: Ecuaciones integrables
Los solitones son soluciones exactas de ecuaciones como:
- KdV (aguas poco profundas).
- Sine-Gordon (ϕtt – ϕxx + sinϕ =0, usada en teoría de campos).
- Schrödinger no lineal (óptica).
El método de transformación inversa de dispersión (desarrollado en 1967) permite resolver estas ecuaciones y predecir interacciones entre solitones.
Interacción entre solitones: ¿Amigos o enemigos?
Cuando dos solitones colisionan:
- Se fusionan temporalmente, creando un perfil complejo.
- Recuperan su forma y velocidad originales tras separarse.
- No hay pérdida de energía, como si fueran partículas elásticas.
Experimento clave: En 1973, los físicos A. Hasegawa y F. Tappert demostraron esto con pulsos láser, confirmando su utilidad en óptica.
Aplicaciones actuales y futuras
| Campo | Aplicación |
|---|---|
| Telecomunicaciones | Fibras ópticas de solitones (usadas en cables submarinos). |
| Medicina | Láseres de solitones para cirugía de precisión. |
| Astrofísica | Modelos de materia oscura como solitones cuánticos (axiones). |
| Nanotecnología | Transporte de electrones en grafeno mediante solitones de carga. |
Límites y desafíos
- Energía requerida: Generar solitones estables en laboratorio exige condiciones extremas (ej: láseres de alta potencia).
- Termalización: En sistemas cuánticos, los solitones pueden perder coherencia debido a interacciones térmicas.
- Detectabilidad: En astrofísica, aún no hay evidencia observacional de solitones de materia oscura.
Conclusión
Los solitones son mucho más que una curiosidad física: son herramientas en telecomunicaciones, laboratorios para estudiar fenómenos cuánticos, y pistas para entender el universo. Como dijo el matemático Clifford S. Gardner: «El solitón es a las ecuaciones no lineales lo que el electrón a la física de partículas: un ladrillo fundamental».