La Magia de la Campana de Gauss
Imagina fenómenos caóticos: el resultado de tirar un dado, el tiempo que tarda un coche en pasar, la cantidad de errores aleatorios. Individualmente, no siguen un patrón. Son puro azar. Pero si tomas suficientes muestras y calculas su promedio, el caos se disuelve. El resultado se alinea bajo la forma más famosa de la estadística: la Campana de Gauss o la Distribución Normal.
Esto no es magia; es la ley de la probabilidad más importante: el Teorema del Límite Central (TLC).
Contexto Histórico: Una Obra Colectiva
El TLC es el resultado de la evolución de la Teoría de la Probabilidad a lo largo de dos siglos:
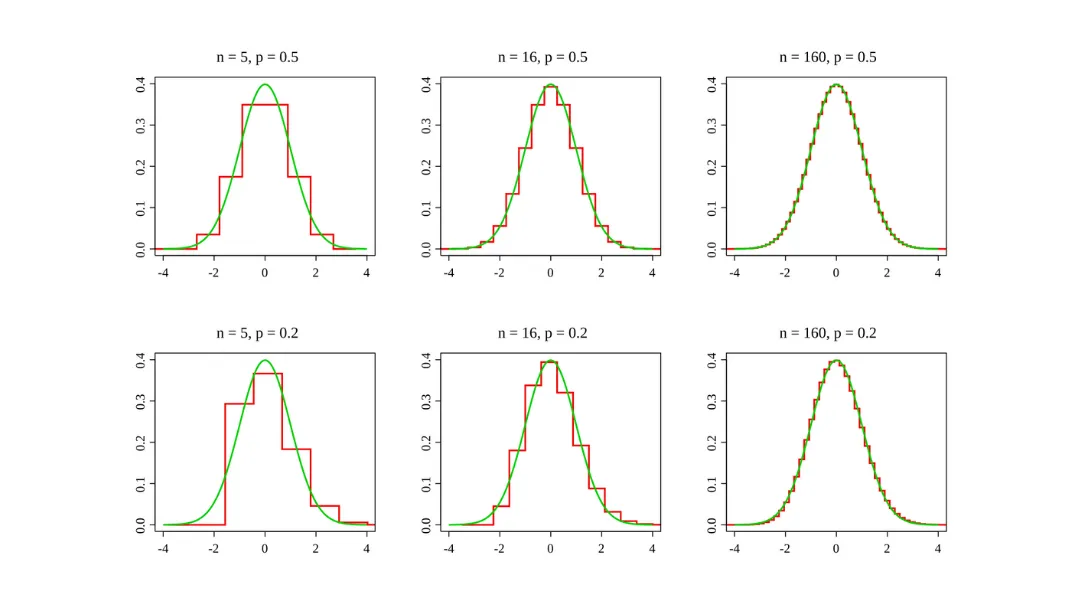
- Abraham de Moivre (S. XVIII) fue el primero en vislumbrar la distribución normal como una aproximación al binomio.
- Pierre-Simon Laplace (Principios del S. XIX) extendió el concepto a una gama más amplia de distribuciones.
- Aleksandr Lyapunov (Principios del S. XX) proporcionó una de las primeras pruebas rigurosas bajo condiciones generales.
La formulación moderna y rigurosa del TLC es la conclusión de estas contribuciones colectivas.
El Enunciado del TLC: La Convergencia a la Normalidad
El Teorema del Límite Central es uno de los resultados más potentes de las Matemáticas.
Enunciado del TLC: Dada una población con media \(\mu\) y desviación estándar \(\sigma\), si tomamos repetidamente muestras aleatorias lo suficientemente grandes (\(n\)) de esa población, la distribución de las medias de esas muestras tenderá a una Distribución Normal.
Las Condiciones Rigurosas
Para que el TLC funcione, se requieren condiciones que aseguren que los datos no sean erráticos:
- Independencia: Cada observación (\(X_i\)) en la muestra debe ser independiente de las otras.
- Varianza Finita: La población original debe tener una varianza (\(\sigma^2\)) que sea finita (los valores no pueden ser infinitamente dispersos).
- Tamaño de Muestra Asintótico: El TLC es estrictamente asintótico, lo que significa que la aproximación es perfecta cuando el tamaño de la muestra (\(n\)) tiende a infinito (\(n \to \infty\)).
Nota Práctica: La regla de \(n \geq 30\) es una heurística popular y útil. Sin embargo, si la distribución original es muy asimétrica (por ejemplo, con sesgos extremos), la aproximación normal requerirá muestras sustancialmente mayores para ser precisa.
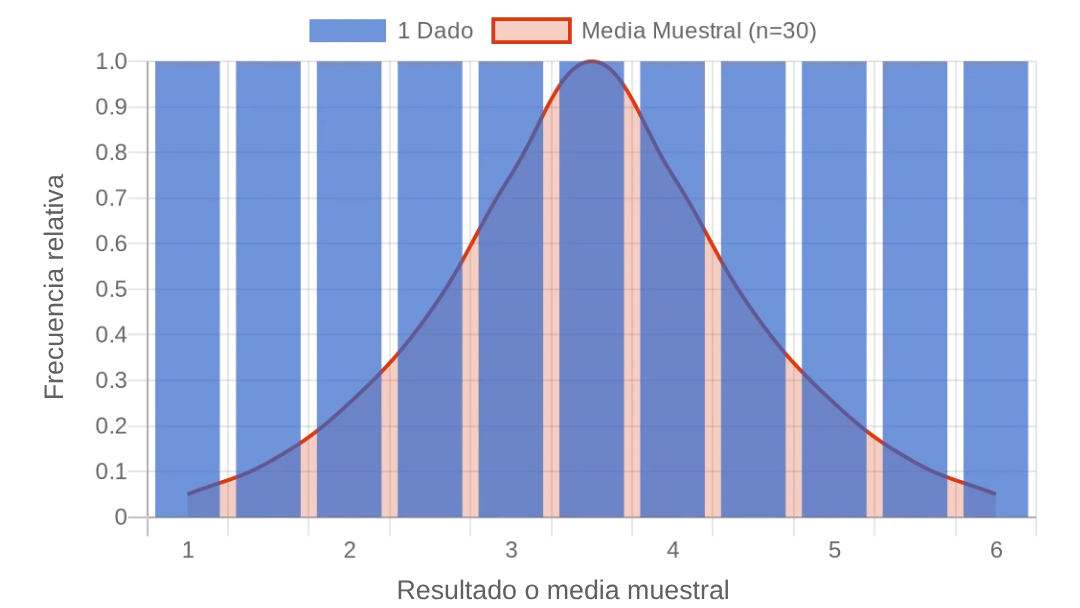
🎲 Ejemplo: El Misterio de los Dados
Imagina tirar un solo dado de 6 caras. La distribución es uniforme (igual probabilidad para 1, 2, 3, 4, 5 o 6).
Ahora, imagina tirar 30 dados y calcular el promedio de los 30 resultados. Repite este experimento miles de veces. La distribución de las medias de estas muestras de 30 dados se aproximará a una normal, centrada en el promedio teórico del dado (3.5). ¡El TLC ha transformado una distribución uniforme en una normal!
TLC y Ley de los Grandes Números
El TLC y la Ley de los Grandes Números (LGN) describen comportamientos complementarios a medida que \(n\) crece:
- Por un lado, la LGN establece que la media de la muestra converge al valor esperado (\(\mu\)), garantizando la precisión de la estimación.
- Por otro lado, el TLC establece la forma de la distribución de esa media. Garantiza que podemos usar la Campana de Gauss para medir la incertidumbre.
La Distribución de las Medias Muestrales
El TLC define la distribución normal resultante con dos parámetros:
- Media de la Muestra: \(\mu_{\bar{x}} = \mu\)
- Error Estándar (Desviación Típica): Mide la dispersión de las medias y se reduce con la raíz cuadrada del tamaño de la muestra:\(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\)
Esta fórmula muestra por qué tomar muestras más grandes hace que la estimación sea más precisa.
Aplicaciones Universales y Tests de Hipótesis
El TLC es el pilar invisible de la estadística inferencial:
- Justificación de Tests Z: El TLC justifica rigurosamente el uso del Test Z para la media muestral en muestras grandes. Debido a que la distribución de la media es normal (gracias al TLC), podemos usar la distribución Z para calcular el valor p y los intervalos de confianza.
- Distinción con el Test T: Es importante señalar que el Test T se usa para muestras pequeñas, asumiendo que la población es normal. Sin embargo, el TLC no es la base fundamental del Test T en muestras pequeñas, aunque la distribución t de Student converge a la normal a medida que \(n\) aumenta.
- Ciencias y Negocios: El TLC valida por qué los promedios de fenómenos complejos (alturas, resultados de pruebas, errores de medición) tienden a ser normales: son el resultado de la suma de innumerables factores independientes.
El Teorema del Límite Central es una ley matemática que garantiza el orden y la previsibilidad a gran escala, la herramienta que nos permite medir el universo.