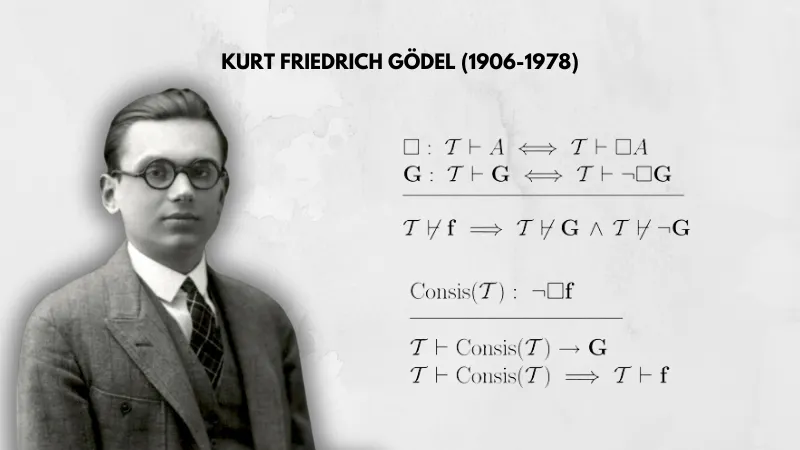Los teoremas de incompletitud de Gödel son dos resultados fundamentales en lógica matemática, presentados en 1931 por el matemático y filósofo austríaco Kurt Gödel. Estos teoremas marcaron un antes y un después en la concepción de las matemáticas y la lógica formal, y sus implicaciones se extienden a diversas disciplinas, como la informática, la teoría de la computación, la filosofía e incluso la inteligencia artificial. A continuación, exploraremos qué son estos teoremas y por qué son tan importantes.
Contexto histórico
En las primeras décadas del siglo XX, uno de los objetivos de la matemática era formalizar todas sus bases, es decir, establecer un conjunto completo y consistente de axiomas desde los cuales pudieran derivarse todas las verdades matemáticas. Este esfuerzo fue parte de un programa más amplio, iniciado por el matemático alemán David Hilbert, conocido como el Programa de Hilbert. La ambición era encontrar un sistema de axiomas que fuera a la vez completo (todas las verdades matemáticas pueden derivarse de él) y consistente (ninguna contradicción puede derivarse de él).
Es aquí donde entran en juego los teoremas de incompletitud de Gödel, que demostraron que este sueño era inalcanzable.
Primer teorema de incompletitud
El primer teorema de incompletitud de Gödel establece que, en cualquier sistema formal suficientemente potente como para incluir la aritmética básica (como el sistema de axiomas de Peano), existen enunciados que son verdaderos pero que no pueden demostrarse dentro de ese sistema. En otras palabras, ningún sistema formal que sea capaz de describir las propiedades de los números naturales puede ser completo: siempre habrá verdades matemáticas que no se pueden probar usando solo los axiomas y reglas de inferencia del sistema.
Este resultado fue asombroso, ya que significaba que las matemáticas contienen inherentemente verdades que escapan a cualquier formalización. Ningún conjunto de reglas puede abarcar todas las verdades sobre los números.
Segundo teorema de incompletitud
El segundo teorema de incompletitud de Gödel va un paso más allá. Afirma que ningún sistema formal coherente que sea suficientemente expresivo para contener la aritmética puede demostrar su propia consistencia. Dicho de otro modo, si un sistema formal es consistente (es decir, no puede derivar una contradicción), esta consistencia no puede ser probada desde dentro del propio sistema. Si queremos probar que un sistema es consistente, necesitamos salir de él, lo que complica aún más la idea de crear una base sólida y segura para las matemáticas.
Implicaciones filosóficas
Los teoremas de incompletitud de Gödel tuvieron un impacto profundo en la filosofía de las matemáticas. Destruyeron la esperanza de formalizar completamente las matemáticas y aseguraron que siempre existirían verdades que no podrían demostrarse. Esto desafía la visión del conocimiento matemático como algo absoluto y completo. Además, influyó en el campo de la teoría del conocimiento al demostrar que hay límites inherentes a lo que podemos conocer, incluso en un campo tan riguroso como las matemáticas.
Influencia en otras áreas
Los teoremas de Gödel no solo afectan a las matemáticas puras. En informática, por ejemplo, están estrechamente relacionados con los límites de lo que las computadoras pueden hacer. La teoría de la computabilidad, desarrollada por Alan Turing, también encontró límites similares al mostrar que existen problemas que no pueden ser resueltos por ninguna máquina, lo que refuerza el espíritu del primer teorema de incompletitud.
En inteligencia artificial, los teoremas de Gödel sugieren que, aunque una máquina pueda llegar a ser increíblemente poderosa en términos de procesamiento, nunca podrá alcanzar una comprensión completa y total de todo. Siempre habrá cosas que escapen a su capacidad de cálculo, tal como sucede con los humanos.
Conclusión
Los teoremas de incompletitud de Gödel cambiaron nuestra comprensión de las matemáticas, la lógica y el conocimiento en general. Nos recuerdan que, aunque las matemáticas son un campo extraordinariamente riguroso, tienen sus propios límites intrínsecos. Las ambiciones de formalizar completamente el conocimiento matemático encontraron un obstáculo insuperable en estos teoremas, y su legado sigue vigente tanto en las matemáticas como en otras disciplinas. Gödel nos enseñó que, al igual que en la vida, en las matemáticas también hay misterios que escapan a nuestra completa comprensión.