El triángulo de Pascal (también conocido como triángulo de Tartaglia) es uno de los diagramas matemáticos más famosos, simple de construir y, sin embargo, rico en patrones matemáticos. Estos se pueden encontrar mediante una búsqueda rápida en la web, pero su descubrimiento mediante el estudio del diagrama es mucho más satisfactorio, y siempre existe la posibilidad de encontrar algo nunca visto.
Una larga historia
El matemático, filósofo y teólogo francés Blaise Pascal fue el primero en hacer un estudio exhaustivo del triángulo. Sin embargo, se conocía mucho tiempo atrás, por eso su diseño no se puede atribuir a un solo individuo. Los primeros matemáticos indios y chinos ya utilizaban este triángulo para la suma de series matemáticas. En India, el patrón fue empleado por primera vez por Pingala (c. 200 a. C.). En China, se encuentra tratado en el libro «Espejo precioso de los cuatro elementos» (1303) de Zhu Shijie. Unos 350 años antes de Pascal, utilizó el triángulo aritmético para la extracción de raíces.
Más tarde, en el mundo islámico, el poeta, astrónomo y matemático persa Omar Khayyam (1048-1131) ideó un método para encontrar raíces basado en la expansión binomial, en cuyo contexto surge naturalmente el triángulo. En Irán, todavía se le llama triángulo de Khayyam.
Si hablamos del concepto binomial (existe una estrecha relación entre el triángulo de Pascal y los binomios de Newton, que podéis ver en este vídeo de unicoos) quizás deberíamos explicar que es un binomio, una expresión que involucra la suma de dos cantidades (a + b). Cuando se multiplica por sí mismo n veces y se expande, los términos individuales del producto son potencias de a y b multiplicadas por coeficientes. El triángulo es una disposición geométrica de estos coeficientes binomiales, que juegan un papel esencial en la teoría de combinaciones y permutaciones. Y Pascal descubrió la importante conexión entre estos coeficientes y la teoría de la probabilidad. Todo un descubrimiento.
Patrones
El matemático británico Godfrey Harold Hardy describió a un matemático como “un hacedor de patrones, como un pintor o un poeta”. De hecho, la búsqueda de patrones que puedan simplificar o unificar los resultados es una preocupación central de la investigación matemática. Podemos ilustrar esta tendencia buscando en el triángulo aritmético.
Aquí tienes una receta para construir el triángulo: coge una hoja grande de papel y escribe las primeras diez o veinte filas. En el centro de la parte superior, escribe 1. Justo debajo, escribe dos 1 más formando un pequeño triángulo. En cada fila siguiente, escribe un 1 en cada extremo y en cada posición entre ellos, escribe la suma de los números de arriba. La figura de arriba muestra las primeras filas del triángulo aritmético. Un estudio de unos minutos revelará varias secuencias de números bien conocidas.
Primero, sumamos los números en cada fila. Encontramos la secuencia 1, 2, 4, 8, 16…, la secuencia de potencias de 2. Ahora mira las diagonales inclinadas de arriba a la derecha a abajo a la izquierda. El primero es solo una secuencia de unos. La siguiente es la secuencia de números naturales: 1, 2, 3, 4…. El tercero da los números triangulares: 1, 3, 6, 10… siendo cada uno una suma de números naturales: 1, 1 + 2, 1 + 2 + 3…. La cuarta diagonal da los números tetraédricos: 1, 4, 10, 20…, el número de puntos necesarios para hacer pirámides con bases triangulares.
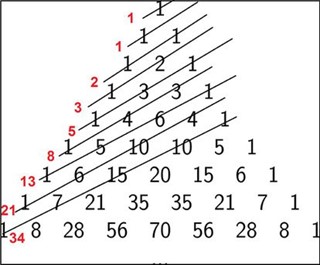Este patrón puede continuar, pero vamos a ver el triángulo de otra manera: sumando los términos de las diagonales, pronto descubrimos la secuencia 1, 1, 2, 3, 5, 8… que algunos lectores pueden reconocer como la secuencia de números de Fibonacci, cada entrada es la suma de los dos números anteriores. Esta notable secuencia aparece en los lugares más inesperados y está estrechamente relacionada con el número áureo, que ha inspirado a los artistas a lo largo de los siglos.
Y numerando las filas del triángulo, comenzando desde 0, y contando los términos en la enésima fila de 0 a n, el número en la posición (n, k) es «n-elige-k«, el número de formas de elegir k elementos de un conjunto de n. Por lo tanto, el número en la posición 5 en la fila 52 es «52-elige-5», el número de posibles manos de póquer. Su valor supera los dos millones y medio.
Más impactante es la cantidad de manos diferentes que puedes tener en una partida de cartas. Es factorial-52, que es aproximadamente… un 8 seguido de 67 ceros. Es tan elevada esta cantidad que es muy posible, que alguna de las veces que hayas jugado, hayas recibido una combinación que nunca en la historia del universo se haya recibido antes.
Otra sorpresa es el patrón fractal que surge si todos los números pares del triángulo se reemplazan por espacios en blanco. En cada escala, el resultado es una aproximación al triángulo de Sierpinski, un conjunto de dimensiones log 2 / log 3.
El triángulo de Pascal, todo un universo matemático quizás todavía por explorar.
Más estudios sobre el triángulo de Pascal continuarán revelando nuevos resultados.
Fuente: That’s Maths
