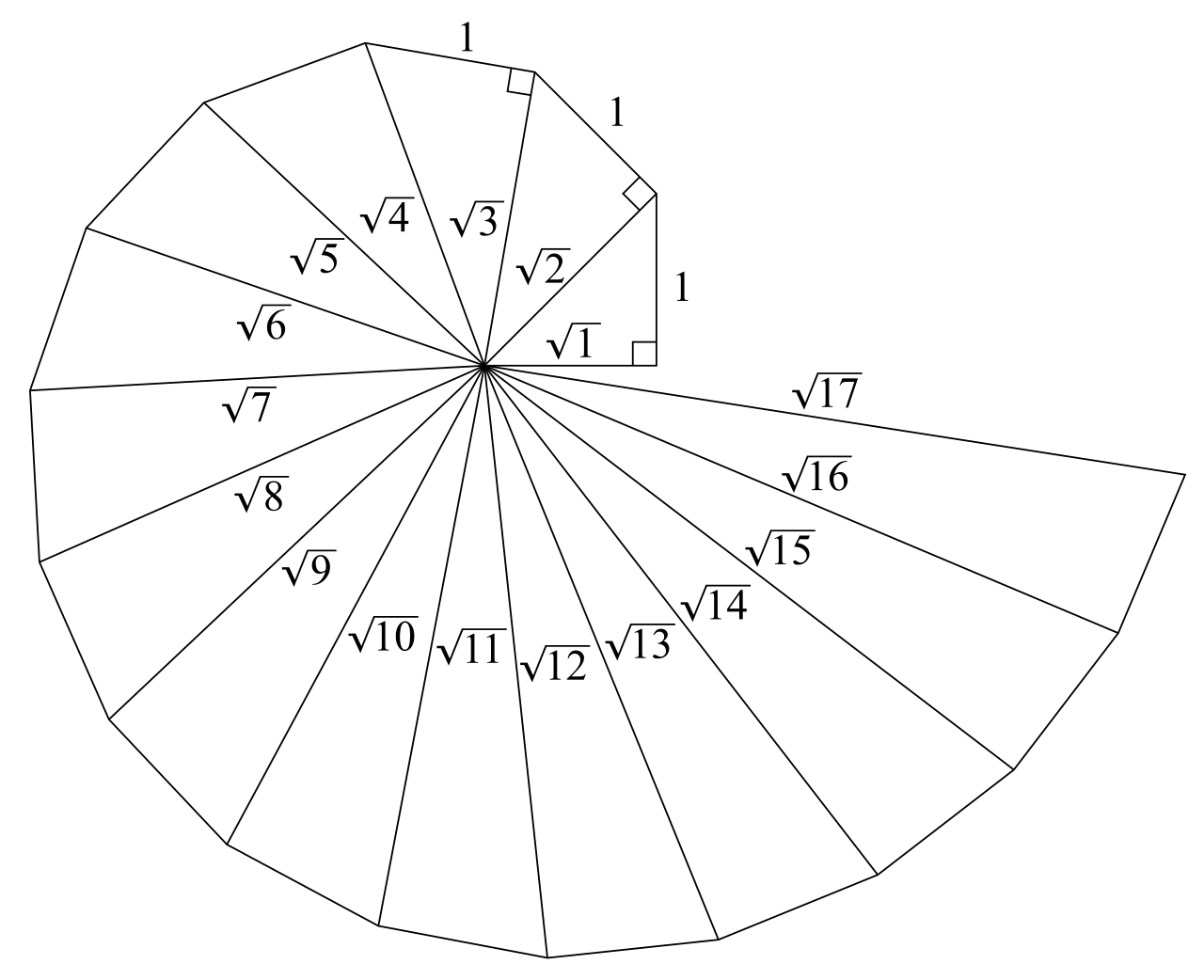
La Espiral de Teodoro, también conocida como caracola pitagórica, espiral pitagórica, espiral de Einstein o espiral de raíces cuadradas, es una fascinante construcción geométrica que revela una serie de cuadrados inscritos en una espiral continua. Este fenómeno matemático, descubierto por primera vez por el matemático griego Teodoro de Cirene, ofrece un interesante vistazo a las relaciones entre los triángulos rectángulos, los cuadrados y las espirales. A continuación, exploramos esta sorprendente figura y sus propiedades únicas.
Una construcción matemática asombrosa
La Espiral de Teodoro se forma al dibujar una serie de cuadrados inscritos en una espiral, donde cada cuadrado tiene su lado igual a la hipotenusa de un triángulo rectángulo cuyos catetos son los lados de los cuadrados previamente dibujados. Esta construcción crea una secuencia infinita de cuadrados que disminuyen en tamaño a medida que la espiral avanza hacia el exterior. La curva resultante es una representación visual de las relaciones geométricas fundamentales entre los lados de los cuadrados y las hipotenusas de los triángulos rectángulos.
Fórmulas y propiedades de la Espiral de Teodoro
Para comprender mejor la Espiral de Teodoro, podemos utilizar una serie de fórmulas que describen las propiedades de los cuadrados y los triángulos rectángulos que la componen. Estas fórmulas nos permiten calcular la longitud de los lados de los cuadrados, la longitud de las hipotenusas de los triángulos rectángulos, el área de cada cuadrado y la longitud total de la espiral hasta un cierto punto. Las fórmulas principales son:
Longitud del Lado del Cuadrado
La longitud del lado del n-ésimo cuadrado, denotada como an, se calcula mediante la fórmula:
![]()
Donde:
- an es la longitud del lado del n-ésimo cuadrado.
- a0 es la longitud del lado del primer cuadrado.
- n es el número de orden del cuadrado.
Longitud de la Hipotenusa del Triángulo Rectángulo
La longitud de la hipotenusa del n-ésimo triángulo rectángulo, denotada como hn, se obtiene con la fórmula:
![]()
Donde:
- ℎn es la longitud de la hipotenusa del n-ésimo triángulo rectángulo.
- a0 es la longitud del lado del primer cuadrado.
- n es el número de orden del cuadrado.
Área del Cuadrado
El área del n-ésimo cuadrado, representada como An, se determina mediante la fórmula:
![]()
Donde:
- An es el área del n-ésimo cuadrado.
- a0 es la longitud del lado del primer cuadrado.
- n es el número de orden del cuadrado.
Suma de las Áreas de los Primeros n Cuadrados
La suma de las áreas de los primeros n cuadrados, denotada como Sn, se calcula con la fórmula:
![]()
Donde:
- Sn es la suma de las áreas de los primeros n cuadrados.
- a0 es la longitud del lado del primer cuadrado.
- n es el número de cuadrados.
Longitud de la Espiral de Teodoro
La longitud de la espiral de Teodoro hasta el n-ésimo cuadrado, representada como Ln, se encuentra mediante la fórmula:

Donde:
- Ln es la longitud de la espiral de Teodoro hasta el n-ésimo cuadrado.
- a0 es la longitud del lado del primer cuadrado.
- n es el número de cuadrados.
Ejemplo práctico de la Espiral de Teodoro
Para ilustrar el uso de estas fórmulas, consideremos un ejemplo práctico. Si el lado del primer cuadrado tiene una longitud de 1 unidad, podemos calcular diversas propiedades de la Espiral de Teodoro hasta un cierto punto. Por ejemplo:
La longitud del lado del segundo cuadrado será:
![]()
La longitud de la hipotenusa del segundo triángulo rectángulo será:
![]()
El área del segundo cuadrado será:
![]()
La suma de las áreas de los dos primeros cuadrados será:
![]()
La longitud de la espiral de Teodoro hasta el segundo cuadrado será:
![]()
Estos cálculos nos proporcionan una comprensión más profunda de la estructura y las propiedades de la Espiral de Teodoro.
Aplicaciones de la Espiral de Teodoro
Arquitectura: La espiral de Teodoro se ha utilizado como elemento decorativo en fachadas y estructuras arquitectónicas. Un ejemplo notable es la fachada del Museo Guggenheim de Bilbao, diseñada por Frank Gehry.
Diseño: La espiral de Teodoro se ha utilizado en el diseño de muebles, textiles, logotipos y otros objetos decorativos. Su forma elegante y armoniosa la hace ideal para crear diseños llamativos y atractivos.
Matemáticas recreativas: La espiral de Teodoro es un objeto de estudio fascinante para las matemáticas recreativas. Se pueden explorar sus propiedades geométricas, como la relación entre la longitud de los lados de los cuadrados y la forma de la espiral.
Otras aplicaciones: La espiral de Teodoro también se ha utilizado en áreas como la física, la ingeniería y la biología. Por ejemplo, se ha utilizado para modelar el crecimiento de las conchas de los caracoles y la forma de las galaxias.